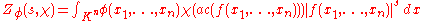Igusa zeta-function
Encyclopedia
In mathematics
, an Igusa zeta function is a type of generating function
, counting the number of solutions of an equation, modulo p, p2, p3, and so on.
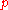let 
be a p-adic field, i.e. 
, 
the valuation ring
and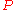
the maximal ideal
. For
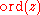denotes the valuation
of
, 
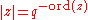, and 
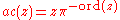for a uniformizing parameter 
of 
.
Furthermore let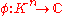
be a Schwartz–Bruhat function, i.e. a locally constant function with compact support and let 
be a character
of
.
In this situation one associates to a non-constant polynomial
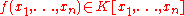the Igusa zeta function
where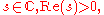
and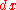 
is Haar measure
so normalized that
has measure 1.
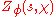is a rational function in 
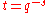. The proof uses Heisuke Hironaka
's theorem about the resolution of singularities
. Later, an entirely different proof was given by Jan Denef
using p-adic cell decomposition. Little is known, however, about explicit formulas. (There are some results about Igusa zeta functions of Fermat varieties.)
Congruences modulo powers of
Henceforth we take 
to be the characteristic function
of
and 
to be the trivial character. Let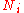 
denote the number of solutions of the congruence
.
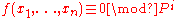Then the Igusa zeta function
is closely related to the Poincaré series
by
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an Igusa zeta function is a type of generating function
Generating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
, counting the number of solutions of an equation, modulo p, p2, p3, and so on.
Definition
For a prime numberPrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
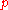let be a p-adic field, i.e. , the valuation ringValuation ring
In abstract algebra, a valuation ring is an integral domain D such that for every element x of its field of fractions F, at least one of x or x −1 belongs to D....
and
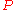the maximal idealIdeal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
. For
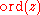denotes the valuationValuation
-Economics:*Valuation , the determination of the economic value of an asset or liability**Real estate appraisal, sometimes called property valuation , the appraisal of land or buildings...
of
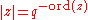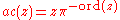, , and for a uniformizing parameter of .Furthermore let
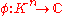be a Schwartz–Bruhat function, i.e. a locally constant function with compact support and let be a characterCharacter (mathematics)
In mathematics, a character is a special kind of function from a group to a field . There are at least two distinct, but overlapping meanings...
of
.In this situation one associates to a non-constant polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
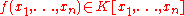the Igusa zeta function
where
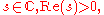and 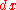is Haar measureHaar measure
In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
so normalized that
has measure 1.Igusa's theorem
showed that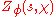 is a rational function in 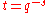. The proof uses Heisuke HironakaHeisuke Hironaka
is a Japanese mathematician. After completing his undergraduate studies at Kyoto University, he received his Ph.D. from Harvard while under the direction of Oscar Zariski. He won the Fields Medal in 1970....
's theorem about the resolution of singularities
Resolution of singularities
In algebraic geometry, the problem of resolution of singularities asks whether every algebraic variety V has a resolution, a non-singular variety W with a proper birational map W→V...
. Later, an entirely different proof was given by Jan Denef
Jan Denef
Jan Denef is a Belgian mathematician. He is Full Professor of Mathematics at the Katholieke Universiteit Leuven.He is a specialist of model theory, number theory and algebraic geometry. He is well known for his early work on Hilbert's tenth problemand for developing the theory of motivic...
using p-adic cell decomposition. Little is known, however, about explicit formulas. (There are some results about Igusa zeta functions of Fermat varieties.)
Congruences modulo powers of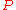 
Henceforth we take to be the characteristic functionCharacteristic function
In mathematics, characteristic function can refer to any of several distinct concepts:* The most common and universal usage is as a synonym for indicator function, that is the function* In probability theory, the characteristic function of any probability distribution on the real line is given by...
of
and to be the trivial character. Let 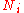denote the number of solutions of the congruenceCongruence relation
In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
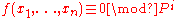.Then the Igusa zeta function
is closely related to the Poincaré series
by
