
Implicant
Encyclopedia
In Boolean logic
, an implicant is a "covering" (sum term or product term) of one or more minterms in a sum of products (or maxterms in a product of sums) of a boolean function. Formally, a product term
P in a sum of products is an implicant of the Boolean function F if P implies F. More precisely:
where
This means that P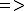 F with respect to the natural ordering of the Boolean space. For instance, the function
F with respect to the natural ordering of the Boolean space. For instance, the function
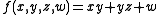
is implied by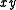 , by
, by 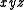 , by
, by 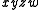 , by
, by 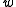 and many others; these are the implicants of
and many others; these are the implicants of 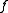 .
.
s) implicant. W.V. Quine defined a prime implicant of F to be an implicant that is minimal - that is, if the removal of any literal from P results in a non-implicant for F. Essential prime implicants are prime implicants that cover an output of the function that no combination of other prime implicants is able to cover.
Using the example above, one can easily see that while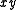 (and others) is a prime implicant,
(and others) is a prime implicant, 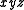 and
and  are not. From the latter, multiple literals can be removed to make it prime:
are not. From the latter, multiple literals can be removed to make it prime:
The process of removing literals from a Boolean term is called expanding the term. Expanding by one literal doubles the number of input combinations for which the term is true (in binary Boolean algebra). Using the example function above, we may expand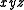 to
to 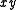 or to
or to 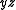 without changing the cover of
without changing the cover of 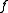 .
.
The sum of all prime implicants of a Boolean function is called the complete sum of that function.
Boolean logic
Boolean algebra is a logical calculus of truth values, developed by George Boole in the 1840s. It resembles the algebra of real numbers, but with the numeric operations of multiplication xy, addition x + y, and negation −x replaced by the respective logical operations of...
, an implicant is a "covering" (sum term or product term) of one or more minterms in a sum of products (or maxterms in a product of sums) of a boolean function. Formally, a product term
Product term
In Boolean logic, a product term is a conjunction of literals, where each literal iseither a variable or its negation. Examples of product terms include:A \wedge BA \wedge \wedge \neg AThe terminology comes from the similarity of AND...
P in a sum of products is an implicant of the Boolean function F if P implies F. More precisely:
- P implies F (and thus is an implicant of F) if F also takes the value 1 whenever P equals 1.
where
- F is a Boolean function of n variables.
- P is a product termProduct termIn Boolean logic, a product term is a conjunction of literals, where each literal iseither a variable or its negation. Examples of product terms include:A \wedge BA \wedge \wedge \neg AThe terminology comes from the similarity of AND...
.
This means that P
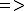 F with respect to the natural ordering of the Boolean space. For instance, the function
F with respect to the natural ordering of the Boolean space. For instance, the function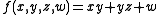
is implied by
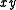 , by
, by 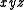 , by
, by 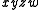 , by
, by 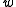 and many others; these are the implicants of
and many others; these are the implicants of 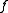 .
.Prime implicant
A prime implicant of a function is an implicant that cannot be covered by a more general (more reduced - meaning with fewer literalLiteral
Literal may refer to:*Literal and figurative language, taken in a non-figurative sense*Literal translation, the close adherence to the forms of a source language text...
s) implicant. W.V. Quine defined a prime implicant of F to be an implicant that is minimal - that is, if the removal of any literal from P results in a non-implicant for F. Essential prime implicants are prime implicants that cover an output of the function that no combination of other prime implicants is able to cover.
Using the example above, one can easily see that while
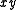 (and others) is a prime implicant,
(and others) is a prime implicant, 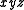 and
and  are not. From the latter, multiple literals can be removed to make it prime:
are not. From the latter, multiple literals can be removed to make it prime: ,
, 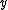 and
and  can be removed, yielding
can be removed, yielding 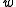 .
.- Alternatively,
 and
and 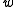 can be removed, yielding
can be removed, yielding 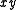 .
. - Finally,
 and
and 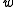 can be removed, yielding
can be removed, yielding 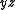 .
.
The process of removing literals from a Boolean term is called expanding the term. Expanding by one literal doubles the number of input combinations for which the term is true (in binary Boolean algebra). Using the example function above, we may expand
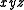 to
to 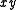 or to
or to 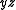 without changing the cover of
without changing the cover of 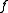 .
. The sum of all prime implicants of a Boolean function is called the complete sum of that function.

