
Inada conditions
Encyclopedia
In macroeconomics
, the Inada conditions (named after Japanese economist Ken-Ichi Inada
) are assumptions about the shape of a production function
that guarantee the stability of an economic growth
path in a neoclassical growth model.
The six conditions for a given function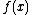 are:
are:
It can be shown that the Inada conditions imply that the production function must be asymptotically Cobb–Douglas.
In stochastic neoclassical growth model if the production function does not satisfy the Inada condition at zero, any feasible path converges to zero with probability one provided that the shocks are sufficiently volatile.
Macroeconomics
Macroeconomics is a branch of economics dealing with the performance, structure, behavior, and decision-making of the whole economy. This includes a national, regional, or global economy...
, the Inada conditions (named after Japanese economist Ken-Ichi Inada
Ken-Ichi Inada
was a Japanese economist.Beginning in the 1950s, Professor Inada wrote a number of important papers on welfare economics, economic growth and international trade. His contributions include an early extension of Kenneth Arrow's impossibility theorem on the existence of a social welfare function...
) are assumptions about the shape of a production function
Production function
In microeconomics and macroeconomics, a production function is a function that specifies the output of a firm, an industry, or an entire economy for all combinations of inputs...
that guarantee the stability of an economic growth
Economic growth
In economics, economic growth is defined as the increasing capacity of the economy to satisfy the wants of goods and services of the members of society. Economic growth is enabled by increases in productivity, which lowers the inputs for a given amount of output. Lowered costs increase demand...
path in a neoclassical growth model.
The six conditions for a given function
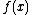 are:
are:- the value of the function
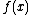 at 0 is 0:
at 0 is 0: 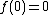
- the function is continuously differentiable,
- the function is strictly increasing in
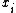 :
: 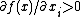 ,
, - the second derivativeDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of the function is decreasing in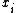 (thus the function is concaveConcave functionIn mathematics, a concave function is the negative of a convex function. A concave function is also synonymously called concave downwards, concave down, convex upwards, convex cap or upper convex.-Definition:...
(thus the function is concaveConcave functionIn mathematics, a concave function is the negative of a convex function. A concave function is also synonymously called concave downwards, concave down, convex upwards, convex cap or upper convex.-Definition:...
): ,
, - the limitLimit of a functionIn mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
of the first derivative is positive infinity as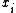 approaches 0:
approaches 0:  ,
, - the limitLimit of a functionIn mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
of the first derivative is zero as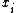 approaches positive infinity:
approaches positive infinity: 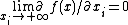
It can be shown that the Inada conditions imply that the production function must be asymptotically Cobb–Douglas.
In stochastic neoclassical growth model if the production function does not satisfy the Inada condition at zero, any feasible path converges to zero with probability one provided that the shocks are sufficiently volatile.

