Indefinite product
Encyclopedia
In mathematics
, the indefinite product operator is the inverse operator of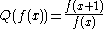
. It is like a discrete version of the indefinite product integral
. Some authors use term discrete multiplicative integration
Thus
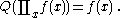
More explicitly, if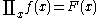
, then
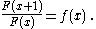
If F(x) is a solution of this functional equation for a given f(x), then so is CF(x) for any constant C. Therefore each indefinite product actually represents a family of functions, differing by a multiplicative constant.
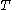is a period of function 
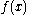then
.
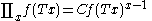
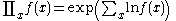
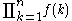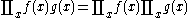
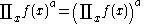
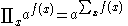
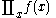. Not all functions have an indefinite product which can be expressed in elementary functions.
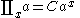
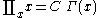
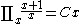
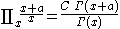
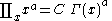
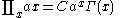
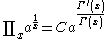
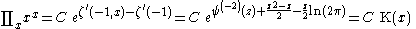
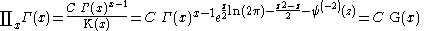
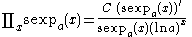
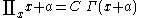
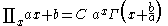
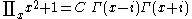
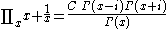
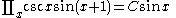
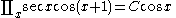
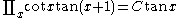
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the indefinite product operator is the inverse operator of
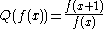. It is like a discrete version of the indefinite product integralProduct integral
Product integrals are a counterpart of standard integrals of infinitesimal calculus. They were first developed by the mathematician Vito Volterra in 1887 to solve systems of linear differential equations...
. Some authors use term discrete multiplicative integration
Thus
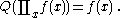
More explicitly, if
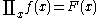, then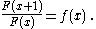If F(x) is a solution of this functional equation for a given f(x), then so is CF(x) for any constant C. Therefore each indefinite product actually represents a family of functions, differing by a multiplicative constant.
Period rule
If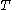 is a period of functio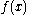n then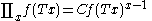Connection to indefinite sum
Indefinite product can be expressed in terms of indefinite sum: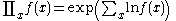Alternative usage
Some authors use the phrase "indefinite product" in a slightly different but related way to describe a product in which the numerical value of the upper limit is not given. e.g.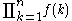.Rules
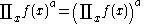
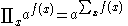
List of indefinite products
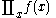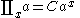
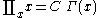
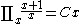
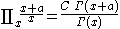
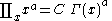
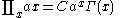
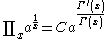
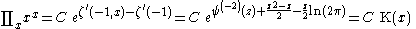
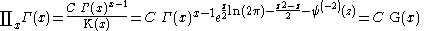
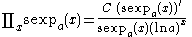
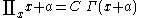
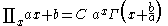
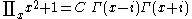
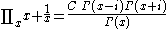
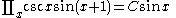
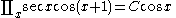
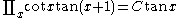
This is a list of indefinite products. Not all functions have an indefinite product which can be expressed in elementary functions.See also
- Indefinite sum
- Product integralProduct integralProduct integrals are a counterpart of standard integrals of infinitesimal calculus. They were first developed by the mathematician Vito Volterra in 1887 to solve systems of linear differential equations...
- Multiplicative calculus#Discrete calculus
- List of derivatives and integrals in alternative calculi
Further reading
- http://reference.wolfram.com/mathematica/ref/Product.html -Indefinite products with Mathematica
- http://www.math.rwth-aachen.de/MapleAnswers/660.html - bug in Maple V to Maple 8 handling of indefinite product
- Markus Müller. How to Add a Non-Integer Number of Terms, and How to Produce Unusual Infinite Summations
- Markus Mueller, Dierk Schleicher. Fractional Sums and Euler-like Identities