Indiana Pi Bill
Encyclopedia
The Indiana Pi Bill is the popular name for bill #246 of the 1897 sitting of the Indiana General Assembly
, one of the most famous attempts to establish scientific truth by legislative fiat. Despite that name, the main result claimed by the bill is a method to square the circle
, rather than to establish a certain value for π
, although the bill does contain text that appears to dictate various incorrect values of π, such as 3.2.
The bill never became law, due to the intervention of a mathematics professor who happened to be present in the legislature.
The impossibility of squaring the circle using only compass and straightedge, suspected since ancient times, was rigorously proved in 1882 by Ferdinand von Lindemann
. Better approximations of π than those inferred from the bill have been known since ancient times.
physician and amateur mathematician Edwin J. Goodwin (ca. 1825 - 1902) believed that he had discovered a correct way of squaring the circle. He proposed a bill to Indiana Representative Taylor I. Record, which Record introduced in the House under the title A Bill for an act introducing a new mathematical truth and offered as a contribution to education to be used only by the State of Indiana free of cost by paying any royalties whatever on the same, provided it is accepted and adopted by the official action of the Legislature of 1897.
The text of the bill consists of a series of mathematical claims (detailed below), followed by a recitation of Goodwin's previous accomplishments:
Goodwin's "solutions" were indeed published in the AMM, though with a disclaimer of 'published by request of the author'.
Upon its introduction in the Indiana House of Representatives
, the bill's language and topic occasioned confusion among the membership; a member from Bloomington
proposed that it be referred to the Finance Committee, but the Speaker accepted another member's recommendation to refer the bill to the Committee on Swamplands, where the bill could "find a deserved grave". It was transferred to the Committee on Education, which reported favorably; following a motion to suspend the rules
, the bill passed on February 6, without a dissenting vote. The news of the bill occasioned an alarmed response from Der Tägliche Telegraph, a German-language
newspaper in Indianapolis, which viewed the event with significantly less favor than its English-speaking competitors. As this debate concluded, Purdue University
Professor C. A. Waldo arrived in Indianapolis
to secure the annual appropriation for the Indiana Academy of Sciences. An assemblyman handed him the bill, offering to introduce him to the genius who wrote it. He declined, saying that he already knew as many crazy people as he cared to.
When it reached the Indiana Senate
, the bill was not treated so kindly. The committee to which it had been assigned reported it unfavorably, and the Senate tabled
it on February 12; it was nearly passed, but opinion changed when one senator observed that the General Assembly lacked the power to define mathematical truth. Influencing some of the senators was a report that major newspapers, such as the Chicago Tribune
, had begun to ridicule the situation.
Although the bill has become known as the "pi bill", its text does not mention the name pi
at all, and Goodwin appears to have thought of the ratio between the circumference and diameter of a circle as distinctly secondary to his main aim of squaring the circle. Towards the end of Section 2 appears the following passage:
This comes close to an explicit claim that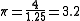
, and that 
.
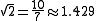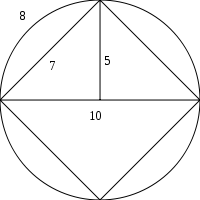
This quotation is often read as three mutually incompatible assertions, but they fit together well if the statement about is taken to be about the inscribed square (with the circle's diameter as diagonal) rather than the square on the radius (with the chord of 90° as diagonal). Together they describe the circle shown in the figure, whose diameter is 10 and circumference is 32; the chord of 90° is taken to be 7. Both of the values 7 and 32 are within a few percent of the true lengths for a diameter-10 circle (which, of course, does not justify Goodwin's presentation of them as exact).
' formula for the area of a circle, which calls for multiplying the diameter by one fourth of the circumference, is not considered a solution to the ancient problem of squaring the circle
. This is because the problem is to construct the area using compass and straightedge
only, and Archimedes did not give a method for constructing a straight line with the same length as the circumference. Goodwin was clearly unaware of this central requirement; he believed that the problem with the Archimedean formula is that it gives wrong numerical results, and that a solution of the ancient problem should consist of replacing it with a "correct" formula. In the bill he proposed, without argument, his own method:
This appears needlessly convoluted, as an "equilateral
rectangle" is, by definition, a square
. In the rest of the bill, however, it is clear that the assertion is simply that area of a circle is the same as that of a square with the same perimeter.
For example, right after the above quote the bill goes on to say:
In the model circle above, the Archimedean area (accepting Goodwin's values for the circumference and diameter) would be 80, whereas Goodwin's proposed rule leads to an area of 64. Now, 80 exceeds 64 by one fifth of 80, and Goodwin appears to confuse 64 = 80×(1−1/5) with 80 = 64×(1+1/5), an approximation that works only for fractions much smaller than 1/5.
The area found by Goodwin's rule is π/4 times the true area of the circle, which in many accounts of the Pi Bill is interpreted as a claim that π = 4. However, there is no internal evidence in the bill that Goodwin intended to make such a claim; on the contrary, he repeatedly denies that the area of the circle has anything to do with its diameter.
The relative area error of 1−π/4 works out to about 21 percent, which is much more grave than the approximations of the lengths in the model circle of the previous section. It is unknown what made Goodwin believe that his rule could be correct. In general, figures with identical perimeters do not have identical area (see isoperimetry
); the typical demonstration of this fact is to compare a long thin shape with small enclosed area (approaching zero as the width decreases) to one of the same perimeter that is approximately as tall as it is wide, obviously of much greater area.
Indiana General Assembly
The Indiana General Assembly is the state legislature, or legislative branch, of the state of Indiana. It is a bicameral legislature that consists of a lower house, the Indiana House of Representatives, and an upper house, the Indiana Senate...
, one of the most famous attempts to establish scientific truth by legislative fiat. Despite that name, the main result claimed by the bill is a method to square the circle
Squaring the circle
Squaring the circle is a problem proposed by ancient geometers. It is the challenge of constructing a square with the same area as a given circle by using only a finite number of steps with compass and straightedge...
, rather than to establish a certain value for π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
, although the bill does contain text that appears to dictate various incorrect values of π, such as 3.2.
The bill never became law, due to the intervention of a mathematics professor who happened to be present in the legislature.
The impossibility of squaring the circle using only compass and straightedge, suspected since ancient times, was rigorously proved in 1882 by Ferdinand von Lindemann
Ferdinand von Lindemann
Carl Louis Ferdinand von Lindemann was a German mathematician, noted for his proof, published in 1882, that π is a transcendental number, i.e., it is not a root of any polynomial with rational coefficients....
. Better approximations of π than those inferred from the bill have been known since ancient times.
Legislative history
In 1897, IndianaIndiana
Indiana is a US state, admitted to the United States as the 19th on December 11, 1816. It is located in the Midwestern United States and Great Lakes Region. With 6,483,802 residents, the state is ranked 15th in population and 16th in population density. Indiana is ranked 38th in land area and is...
physician and amateur mathematician Edwin J. Goodwin (ca. 1825 - 1902) believed that he had discovered a correct way of squaring the circle. He proposed a bill to Indiana Representative Taylor I. Record, which Record introduced in the House under the title A Bill for an act introducing a new mathematical truth and offered as a contribution to education to be used only by the State of Indiana free of cost by paying any royalties whatever on the same, provided it is accepted and adopted by the official action of the Legislature of 1897.
The text of the bill consists of a series of mathematical claims (detailed below), followed by a recitation of Goodwin's previous accomplishments:
Goodwin's "solutions" were indeed published in the AMM, though with a disclaimer of 'published by request of the author'.
Upon its introduction in the Indiana House of Representatives
Indiana House of Representatives
The Indiana House of Representatives is the lower house of the Indiana General Assembly, the state legislature of the U.S. state of Indiana. The House is composed of 100 members representing an equal number of constituent districts. House members serve two-year terms without term limits...
, the bill's language and topic occasioned confusion among the membership; a member from Bloomington
Bloomington, Indiana
Bloomington is a city in and the county seat of Monroe County in the southern region of the U.S. state of Indiana. The population was 80,405 at the 2010 census....
proposed that it be referred to the Finance Committee, but the Speaker accepted another member's recommendation to refer the bill to the Committee on Swamplands, where the bill could "find a deserved grave". It was transferred to the Committee on Education, which reported favorably; following a motion to suspend the rules
Suspension of the rules
Suspension of the rules in the United States Congress is the specific set of procedures within the United States Congress that allows for the general parliamentary procedure notion of how and when to suspend the rules.-Overview:...
, the bill passed on February 6, without a dissenting vote. The news of the bill occasioned an alarmed response from Der Tägliche Telegraph, a German-language
German language
German is a West Germanic language, related to and classified alongside English and Dutch. With an estimated 90 – 98 million native speakers, German is one of the world's major languages and is the most widely-spoken first language in the European Union....
newspaper in Indianapolis, which viewed the event with significantly less favor than its English-speaking competitors. As this debate concluded, Purdue University
Purdue University
Purdue University, located in West Lafayette, Indiana, U.S., is the flagship university of the six-campus Purdue University system. Purdue was founded on May 6, 1869, as a land-grant university when the Indiana General Assembly, taking advantage of the Morrill Act, accepted a donation of land and...
Professor C. A. Waldo arrived in Indianapolis
Indianapolis
Indianapolis is the capital of the U.S. state of Indiana, and the county seat of Marion County, Indiana. As of the 2010 United States Census, the city's population is 839,489. It is by far Indiana's largest city and, as of the 2010 U.S...
to secure the annual appropriation for the Indiana Academy of Sciences. An assemblyman handed him the bill, offering to introduce him to the genius who wrote it. He declined, saying that he already knew as many crazy people as he cared to.
When it reached the Indiana Senate
Indiana Senate
The Indiana Senate is the upper house of the Indiana General Assembly, the state legislature of the U.S. state of Indiana. The Senate is composed of 50 members representing an equal number of constituent districts. Senators serve four-year terms without term limits...
, the bill was not treated so kindly. The committee to which it had been assigned reported it unfavorably, and the Senate tabled
Table (parliamentary procedure)
In parliamentary procedure, a motion to table has two different and contradictory meanings:*In the United States, table usually means the motion to lay on the table or motion to postpone consideration; a proposal to suspend consideration of a pending motion...
it on February 12; it was nearly passed, but opinion changed when one senator observed that the General Assembly lacked the power to define mathematical truth. Influencing some of the senators was a report that major newspapers, such as the Chicago Tribune
Chicago Tribune
The Chicago Tribune is a major daily newspaper based in Chicago, Illinois, and the flagship publication of the Tribune Company. Formerly self-styled as the "World's Greatest Newspaper" , it remains the most read daily newspaper of the Chicago metropolitan area and the Great Lakes region and is...
, had begun to ridicule the situation.
Approximation of π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
at all, and Goodwin appears to have thought of the ratio between the circumference and diameter of a circle as distinctly secondary to his main aim of squaring the circle. Towards the end of Section 2 appears the following passage:
This comes close to an explicit claim that
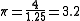, and that 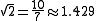.This quotation is often read as three mutually incompatible assertions, but they fit together well if the statement about is taken to be about the inscribed square (with the circle's diameter as diagonal) rather than the square on the radius (with the chord of 90° as diagonal). Together they describe the circle shown in the figure, whose diameter is 10 and circumference is 32; the chord of 90° is taken to be 7. Both of the values 7 and 32 are within a few percent of the true lengths for a diameter-10 circle (which, of course, does not justify Goodwin's presentation of them as exact).
Area of the circle
Goodwin's main goal was not to measure lengths in the circle but to square it, which he interpreted literally as finding a square with the same area as the circle. He knew that ArchimedesArchimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
' formula for the area of a circle, which calls for multiplying the diameter by one fourth of the circumference, is not considered a solution to the ancient problem of squaring the circle
Squaring the circle
Squaring the circle is a problem proposed by ancient geometers. It is the challenge of constructing a square with the same area as a given circle by using only a finite number of steps with compass and straightedge...
. This is because the problem is to construct the area using compass and straightedge
Compass and straightedge
Compass-and-straightedge or ruler-and-compass construction is the construction of lengths, angles, and other geometric figures using only an idealized ruler and compass....
only, and Archimedes did not give a method for constructing a straight line with the same length as the circumference. Goodwin was clearly unaware of this central requirement; he believed that the problem with the Archimedean formula is that it gives wrong numerical results, and that a solution of the ancient problem should consist of replacing it with a "correct" formula. In the bill he proposed, without argument, his own method:
This appears needlessly convoluted, as an "equilateral
Equilateral
In geometry, an equilateral polygon is a polygon which has all sides of the same length.For instance, an equilateral triangle is a triangle of equal edge lengths...
rectangle" is, by definition, a square
Square
-Mathematics and science:* Square , a cryptographic block cipher* Square , a regular quadrilateral with four equal sides and four right angles* Square number, an integer that is the square of another integer-Construction:...
. In the rest of the bill, however, it is clear that the assertion is simply that area of a circle is the same as that of a square with the same perimeter.
For example, right after the above quote the bill goes on to say:
In the model circle above, the Archimedean area (accepting Goodwin's values for the circumference and diameter) would be 80, whereas Goodwin's proposed rule leads to an area of 64. Now, 80 exceeds 64 by one fifth of 80, and Goodwin appears to confuse 64 = 80×(1−1/5) with 80 = 64×(1+1/5), an approximation that works only for fractions much smaller than 1/5.
The area found by Goodwin's rule is π/4 times the true area of the circle, which in many accounts of the Pi Bill is interpreted as a claim that π = 4. However, there is no internal evidence in the bill that Goodwin intended to make such a claim; on the contrary, he repeatedly denies that the area of the circle has anything to do with its diameter.
The relative area error of 1−π/4 works out to about 21 percent, which is much more grave than the approximations of the lengths in the model circle of the previous section. It is unknown what made Goodwin believe that his rule could be correct. In general, figures with identical perimeters do not have identical area (see isoperimetry
Isoperimetry
The isoperimetric inequality is a geometric inequality involving the square of the circumference of a closed curve in the plane and the area of a plane region it encloses, as well as its various generalizations. Isoperimetric literally means "having the same perimeter"...
); the typical demonstration of this fact is to compare a long thin shape with small enclosed area (approaching zero as the width decreases) to one of the same perimeter that is approximately as tall as it is wide, obviously of much greater area.
External links
- Full text of the bill
- Indiana Pi narrative about the near-passing of the bill
- The Straight Dope article
- Alabama Changes the Value of Pi related hoax