.gif)
Indra's Pearls (book)
Encyclopedia
Indra's Pearls: The Vision of Felix Klein is a geometry
book written by David Mumford
, Caroline Series and David Wright, and published by Cambridge University Press
in 2002.
The book explores the patterns created by iterating conformal map
s of the complex plane
called Möbius transformations, and their connections with symmetry
and self-similarity. These patterns were glimpsed by German
mathematician
Felix Klein
, but modern computer graphics allows them to be fully visualised and explored in detail.
, a metaphorical object described in the Buddhist
text of the Flower Garland Sutra. Indra's net consists of an infinite array of gossamer strands and pearls. The frontispiece to Indra's Pearls quotes the following description:
The allusion to Felix Klein's "vision" is a reference to Klein's early investigations of Schottky group
s and hand-drawn plots of their limit sets. It also refers to Klein's wider vision of the connections between group theory
, symmetry and geometry - see Erlangen program
.
, number theory
, abstract algebra
and computer graphics
. It shows how computers are used by contemporary mathematicians. It uses computer graphics, diagrams and cartoons to enhance its written explanations. In the authors' own words:
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
book written by David Mumford
David Mumford
David Bryant Mumford is an American mathematician known for distinguished work in algebraic geometry, and then for research into vision and pattern theory. He won the Fields Medal and was a MacArthur Fellow. In 2010 he was awarded the National Medal of Science...
, Caroline Series and David Wright, and published by Cambridge University Press
Cambridge University Press
Cambridge University Press is the publishing business of the University of Cambridge. Granted letters patent by Henry VIII in 1534, it is the world's oldest publishing house, and the second largest university press in the world...
in 2002.
The book explores the patterns created by iterating conformal map
Conformal map
In mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...
s of the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
called Möbius transformations, and their connections with symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
and self-similarity. These patterns were glimpsed by German
Germany
Germany , officially the Federal Republic of Germany , is a federal parliamentary republic in Europe. The country consists of 16 states while the capital and largest city is Berlin. Germany covers an area of 357,021 km2 and has a largely temperate seasonal climate...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Felix Klein
Felix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
, but modern computer graphics allows them to be fully visualised and explored in detail.
Title
The book's title refers to Indra's netIndra's net
Indra's net is a metaphor used to illustrate the concepts of emptiness, dependent origination, and interpenetration in Buddhist philosophy...
, a metaphorical object described in the Buddhist
Buddhism
Buddhism is a religion and philosophy encompassing a variety of traditions, beliefs and practices, largely based on teachings attributed to Siddhartha Gautama, commonly known as the Buddha . The Buddha lived and taught in the northeastern Indian subcontinent some time between the 6th and 4th...
text of the Flower Garland Sutra. Indra's net consists of an infinite array of gossamer strands and pearls. The frontispiece to Indra's Pearls quotes the following description:
- In the glistening surface of each pearl are reflected all the other pearls ... In each reflection, again are reflected all the infinitely many other pearls, so that by this process, reflections of reflections continue without end.
The allusion to Felix Klein's "vision" is a reference to Klein's early investigations of Schottky group
Schottky group
In mathematics, a Schottky group is a special sort of Kleinian group, first studied by .-Definition:Fix some point p on the Riemann sphere...
s and hand-drawn plots of their limit sets. It also refers to Klein's wider vision of the connections between group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, symmetry and geometry - see Erlangen program
Erlangen program
An influential research program and manifesto was published in 1872 by Felix Klein, under the title Vergleichende Betrachtungen über neuere geometrische Forschungen...
.
Contents
The contents of Indra's Pearls are as follows:
- Chapter 1. The language of symmetry – an introduction to the mathematical concept of symmetry and its relation to geometric groups.
- Chapter 2. A delightful fiction – an introduction to complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s and mappings of the complex plane and the Riemann sphereRiemann sphereIn mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
. - Chapter 3. Double spirals and Möbius maps – Möbius transformations and their classification.
- Chapter 4. The Schottky dance – pairs of Möbius maps which generate Schottky groups; plotting their limit setLimit setIn mathematics, especially in the study of dynamical systems, a limit set is the state a dynamical system reaches after an infinite amount of time has passed, by either going forward or backwards in time...
s using breadth-first searchBreadth-first searchIn graph theory, breadth-first search is a graph search algorithm that begins at the root node and explores all the neighboring nodes...
es. - Chapter 5. Fractal dust and infinite words – Schottky limit sets regarded as fractalFractalA fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
s; computer generation of these fractals using depth-first searchDepth-first searchDepth-first search is an algorithm for traversing or searching a tree, tree structure, or graph. One starts at the root and explores as far as possible along each branch before backtracking....
es and iterated function systemIterated function systemIn mathematics, iterated function systems or IFSs are a method of constructing fractals; the resulting constructions are always self-similar....
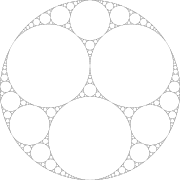
s. - Chapter 6. Indra's necklace – the continuous limit sets generated when pairs of generating circles touch.
- Chapter 7. The glowing gasket – the Schottky group whose limit set is the Apollonian gasketApollonian gasketIn mathematics, an Apollonian gasket or Apollonian net is a fractal generated from triples of circles, where each circle is tangent to the other two. It is named after Greek mathematician Apollonius of Perga.-Construction:...
; links to the modular groupModular groupIn mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
. - Chapter 8. Playing with parameters – parameterising Schottky groups with parabolicParabolaIn mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
commutatorCommutatorIn mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
using two complex parameters; using these parameters to explore the Teichmüller spaceTeichmüller spaceIn mathematics, the Teichmüller space TX of a topological surface X, is a space that parameterizes complex structures on X up to the action of homeomorphisms that are isotopic to the identity homeomorphism...
of Schottky groups. - Chapter 9. Accidents will happen – introducing Maskit's slice, parameterised by a single complex parameter; exploring the boundary between discrete and non-discrete groups.
- Chapter 10. Between the cracks – further exploration of the Maskit boundary between discrete and non-discrete groups in another slice of parameter space; identification and exploration of degenerate groups.
- Chapter 11. Crossing boundaries – ideas for further exploration, such as adding a third generator.
- Chapter 12. Epilogue – concluding overview of non-Euclidean geometryNon-Euclidean geometryNon-Euclidean geometry is the term used to refer to two specific geometries which are, loosely speaking, obtained by negating the Euclidean parallel postulate, namely hyperbolic and elliptic geometry. This is one term which, for historical reasons, has a meaning in mathematics which is much...
and Teichmüller theory.
Importance
Indra's Pearls is unusual because it aims to give the reader a sense of the development of a real-life mathematical investigation, rather than just a formal presentation of the final results. It covers a broad span of topics, showing interconnections among geometryGeometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
and computer graphics
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
. It shows how computers are used by contemporary mathematicians. It uses computer graphics, diagrams and cartoons to enhance its written explanations. In the authors' own words:
- Our dream is that this book will reveal to our readers that mathematics is not alien and remote but just a very human exploration of the patterns of the world, one which thrives on play and surprise and beauty - Indra's Pearls p viii.

