Infinite-dimensional holomorphy
Encyclopedia
In mathematics
, infinite-dimensional holomorphy is a branch of functional analysis
. It is concerned with generalizations of the concept of holomorphic function
to functions defined and taking values in complex
Banach space
s (or Fréchet spaces more generally), typically of infinite dimension. It is one aspect of nonlinear functional analysis
.
C, but take values in a Banach space. Such functions are important, for example, in constructing the holomorphic functional calculus
for bounded linear operators.
A function f:U→X defined on an open subset U of the complex plane with values in a complex Banach space X is called holomorphic if it is complex-differentiable; that is, for each point z in U the limit
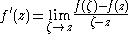
exists.
One may define the line integral
of a vector-valued holomorphic function f:U→X along a rectifiable curve γ [a, b]→ U in the same way as for complex-valued holomorphic functions, as the limit of sums of the form
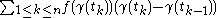
where a = t0 < t1 < ... < tn = b is a subdivision of the interval [a, b], as the lengths of the subdivision intervals approach zero.
It is a quick check that the Cauchy integral theorem also holds for vector-valued holomorphic functions. Indeed, if f:U→X is such a function and T:X→C a bounded linear operator, one can show that
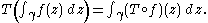
Moreover, the composition
Tof:U→C is a complex-valued holomorphic function. Therefore, for γ a simple closed curve whose interior is contained in U, the integral on the right is zero, by the classical Cauchy integral theorem. Then, since T is arbitrary, it follows from the Hahn–Banach theorem
that
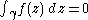
which proves the Cauchy integral theorem in the vector-valued case.
Using this powerful tool one may then prove Cauchy's integral formula
, and, just like in the classical case, that any vector-valued holomorphic function is analytic
.
A useful criterion for a function f : U → X to be holomorphic is that T o f : U → C is a holomorphic complex-valued function for every continuous linear functional T : X → C. Such an f is weakly
holomorphic. It can be shown that a function defined on an open subset of the complex plane with values in a Fréchet space is holomorphic if, and only if, it is weakly holomorphic.
s X and Y over the complex numbers and an open set U in X, f : U → Y is called holomorphic if the Fréchet derivative
of f exists at every point in U. One can show that, in this more general context, it is still true that a holomorphic function is analytic, that is, it can be locally expanded in a power series. It is no longer true however that if a function is defined and holomorphic in a ball, its power series around the center of the ball is convergent in the entire ball; for example, there exist holomorphic functions defined on the entire space which have a finite radius of convergence.
s X and Y over the complex numbers and an open set U in X, there are various ways of defining holomorphy of a function f : U → Y. Unlike the finite dimensional setting, when X and Y are infinite dimensional, the properties of holomorphic functions may depend on which definition is chosen. To restrict the number of possibilities we must consider, we shall only discuss holomorphy in the case when X and Y are locally convex.
This section presents a list of definitions, proceeding from the weakest notion to the strongest notion. It concludes with a discussion of some theorems relating these definitions when the spaces X and Y satisfy some additional constraints.
Let X and Y be locally convex topological vector spaces, and U ⊂ X an open set. A function f : U → Y is said to be Gâteaux holomorphic if, for every a ∈ U and b ∈ X, and every continuous linear functional φ on Y, the function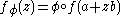
is a holomorphic function of z in a neighborhood of z = 0. The collection of Gâteaux holomorphic functions is denoted by HG(U,Y).
In the analysis of Gâteaux holomorphic functions, any properties of finite-dimensional holomorphic functions hold on finite-dimensional subspaces of X. However, as usual in functional analysis, these properties may not piece together uniformly to yield any corresponding properties of these functions on full open sets.
Examples:
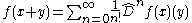
(which is already guaranteed to exist by Gâteaux holomorphy) converges and is continuous for y in a neighborhood of 0 ∈ X. Thus holomorphy combines the notion of weak holomorphy with the convergence of the power series expansion. The collection of holomorphic functions is denoted by H(U,Y).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, infinite-dimensional holomorphy is a branch of functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
. It is concerned with generalizations of the concept of holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
to functions defined and taking values in complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s (or Fréchet spaces more generally), typically of infinite dimension. It is one aspect of nonlinear functional analysis
Nonlinear functional analysis
Nonlinear functional analysis is a branch of Mathematical Analysis. It deals with nonlinear mappings and its subject matter includes:* generalizations of calculus to Banach spaces* implicit function theorems...
.
Vector-valued holomorphic functions defined in the complex plane
A first step in extending the theory of holomorphic functions beyond one complex dimension is considering so-called vector-valued holomorphic functions, which are still defined in the complex planeComplex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
C, but take values in a Banach space. Such functions are important, for example, in constructing the holomorphic functional calculus
Holomorphic functional calculus
In mathematics, holomorphic functional calculus is functional calculus with holomorphic functions. That is to say, given a holomorphic function ƒ of a complex argument z and an operator T, the aim is to construct an operatorf\,...
for bounded linear operators.
A function f:U→X defined on an open subset U of the complex plane with values in a complex Banach space X is called holomorphic if it is complex-differentiable; that is, for each point z in U the limit
Limit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
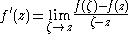
exists.
One may define the line integral
Line integral
In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field...
of a vector-valued holomorphic function f:U→X along a rectifiable curve γ [a, b]→ U in the same way as for complex-valued holomorphic functions, as the limit of sums of the form
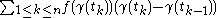
where a = t0 < t1 < ... < tn = b is a subdivision of the interval [a, b], as the lengths of the subdivision intervals approach zero.
It is a quick check that the Cauchy integral theorem also holds for vector-valued holomorphic functions. Indeed, if f:U→X is such a function and T:X→C a bounded linear operator, one can show that
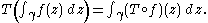
Moreover, the composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
Tof:U→C is a complex-valued holomorphic function. Therefore, for γ a simple closed curve whose interior is contained in U, the integral on the right is zero, by the classical Cauchy integral theorem. Then, since T is arbitrary, it follows from the Hahn–Banach theorem
Hahn–Banach theorem
In mathematics, the Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed...
that
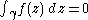
which proves the Cauchy integral theorem in the vector-valued case.
Using this powerful tool one may then prove Cauchy's integral formula
Cauchy's integral formula
In mathematics, Cauchy's integral formula, named after Augustin-Louis Cauchy, is a central statement in complex analysis. It expresses the fact that a holomorphic function defined on a disk is completely determined by its values on the boundary of the disk, and it provides integral formulas for all...
, and, just like in the classical case, that any vector-valued holomorphic function is analytic
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
.
A useful criterion for a function f : U → X to be holomorphic is that T o f : U → C is a holomorphic complex-valued function for every continuous linear functional T : X → C. Such an f is weakly
Weak topology
In mathematics, weak topology is an alternative term for initial topology. The term is most commonly used for the initial topology of a topological vector space with respect to its continuous dual...
holomorphic. It can be shown that a function defined on an open subset of the complex plane with values in a Fréchet space is holomorphic if, and only if, it is weakly holomorphic.
Holomorphic functions between Banach spaces
More generally, given two Banach spaceBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s X and Y over the complex numbers and an open set U in X, f : U → Y is called holomorphic if the Fréchet derivative
Fréchet derivative
In mathematics, the Fréchet derivative is a derivative defined on Banach spaces. Named after Maurice Fréchet, it is commonly used to formalize the concept of the functional derivative used widely in the calculus of variations. Intuitively, it generalizes the idea of linear approximation from...
of f exists at every point in U. One can show that, in this more general context, it is still true that a holomorphic function is analytic, that is, it can be locally expanded in a power series. It is no longer true however that if a function is defined and holomorphic in a ball, its power series around the center of the ball is convergent in the entire ball; for example, there exist holomorphic functions defined on the entire space which have a finite radius of convergence.
Holomorphic functions between topological vector spaces
In the fully general situation, given two topological vector spaceTopological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
s X and Y over the complex numbers and an open set U in X, there are various ways of defining holomorphy of a function f : U → Y. Unlike the finite dimensional setting, when X and Y are infinite dimensional, the properties of holomorphic functions may depend on which definition is chosen. To restrict the number of possibilities we must consider, we shall only discuss holomorphy in the case when X and Y are locally convex.
This section presents a list of definitions, proceeding from the weakest notion to the strongest notion. It concludes with a discussion of some theorems relating these definitions when the spaces X and Y satisfy some additional constraints.
Gâteaux holomorphy
Gâteaux holomorphy is the direct generalization of weak holomorphy to the fully infinite dimensional setting.Let X and Y be locally convex topological vector spaces, and U ⊂ X an open set. A function f : U → Y is said to be Gâteaux holomorphic if, for every a ∈ U and b ∈ X, and every continuous linear functional φ on Y, the function
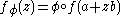
is a holomorphic function of z in a neighborhood of z = 0. The collection of Gâteaux holomorphic functions is denoted by HG(U,Y).
In the analysis of Gâteaux holomorphic functions, any properties of finite-dimensional holomorphic functions hold on finite-dimensional subspaces of X. However, as usual in functional analysis, these properties may not piece together uniformly to yield any corresponding properties of these functions on full open sets.
Examples:
- If f ∈ U, then f has Gâteaux derivativeGâteaux derivativeIn mathematics, the Gâteaux differential or Gâteaux derivative is a generalization of the concept of directional derivative in differential calculus. Named after René Gâteaux, a French mathematician who died young in World War I, it is defined for functions between locally convex topological vector...
s of all orders, since for x ∈ U and h1, ..., hk ∈ X, the k-th order Gâteaux derivative Dkf(x){h1,...,hk} involves only iterated directional derivatives in the span of the hi, which is a finite-dimensional space. In this case, the iterated Gâteaux derivatives are multilinear in the hi, but will in general fail to be continuous when regarded over the whole space X.
- Furthermore, a version of Taylor's theorem holds:
- Here,
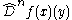is the homogeneous polynomialHomogeneous polynomialIn mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
of degree n in y associated with the multilinear operator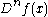
. The convergence of this series is not uniform. More precisely, if V ⊂ X is a fixed finite-dimensional subspace, then the series converges uniformly on sufficiently small compact neighborhoods of 0 ∈ Y. However, if the subspace V is permitted to vary, then the convergence fails: it will in general fail to be uniform with respect to this variation. Note that this is in sharp contrast with the finite dimensional case.
- Hartog's theorem holds for Gâteaux holomorphic functions in the following sense:
- If f : (U⊂ X1) × (V⊂ X2) → Y is a function which is separately Gâteaux holomorphic in each of its arguments, then f is Gâteaux holomorphic on the product space.
Hypoanalyticity
A function f : (U ⊂ X) → Y is hypoanalytic if f ∈ HG(U,Y) and in addition f is continuous on relatively compact subsets of U.Holomorphy
A function f ∈ HG(U,Y) is holomorphic if, for every x ∈ U, the Taylor series expansion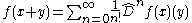(which is already guaranteed to exist by Gâteaux holomorphy) converges and is continuous for y in a neighborhood of 0 ∈ X. Thus holomorphy combines the notion of weak holomorphy with the convergence of the power series expansion. The collection of holomorphic functions is denoted by H(U,Y).