Integer matrix
Encyclopedia
In mathematics
, an integer matrix is a matrix
whose entries are all integer
s. Examples include binary matrices, the zero matrix, the unit matrix, and the adjacency matrices
used in graph theory
, amongst many others. Integer matrices find frequent application in combinatorics
.
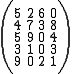and 
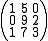
are both examples of integer matrices.
of an integer matrix is itself an integer, thus the smallest possible magnitude of the determinant of an invertible integer matrix is one, hence where inverses exist they do not become excessively large (see condition number
). Theorems from matrix theory that infer properties from determinants thus avoid the traps induced by ill conditioned (nearly zero determinant) real or floating point
valued matrices.
The inverse of an integer matrix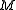
is again an integer matrix if and only if the determinant of 
is exactly 
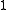or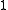 
. Integer matrices of determinant 
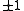form the group 
, which has far-reaching applications in arithmetic and geometry. For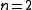 
, it is closely related to the modular group
.
The intersection of the integer matrices with the orthogonal group
is the group of signed permutation matrices.
The characteristic polynomial
of an integer matrix has integer coefficients. Since the eigenvalues of a matrix are the roots of the polynomial, the eigenvalues of an integer matrix are algebraic integers. In dimension less than 5, they can thus be expressed by radicals
involving integers.
Integer matrices are sometimes called integral matrices, although this use is discouraged.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an integer matrix is a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
whose entries are all integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s. Examples include binary matrices, the zero matrix, the unit matrix, and the adjacency matrices
Adjacency matrix
In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
used in graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, amongst many others. Integer matrices find frequent application in combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
.
Examples
and 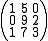are both examples of integer matrices.
Properties
Invertibility of integer matrices is in general more numerically stable than that of non-integer matrices. The determinantDeterminant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of an integer matrix is itself an integer, thus the smallest possible magnitude of the determinant of an invertible integer matrix is one, hence where inverses exist they do not become excessively large (see condition number
Condition number
In the field of numerical analysis, the condition number of a function with respect to an argument measures the asymptotically worst case of how much the function can change in proportion to small changes in the argument...
). Theorems from matrix theory that infer properties from determinants thus avoid the traps induced by ill conditioned (nearly zero determinant) real or floating point
Floating point
In computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...
valued matrices.
The inverse of an integer matrix
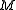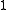is again an integer matrix if and only if the determinant of is exactly or 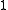. Integer matrices of determinant 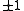form the group , which has far-reaching applications in arithmetic and geometry. For 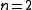, it is closely related to the modular groupModular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
.
The intersection of the integer matrices with the orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
is the group of signed permutation matrices.
The characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of an integer matrix has integer coefficients. Since the eigenvalues of a matrix are the roots of the polynomial, the eigenvalues of an integer matrix are algebraic integers. In dimension less than 5, they can thus be expressed by radicals
Nth root
In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
involving integers.
Integer matrices are sometimes called integral matrices, although this use is discouraged.