
Integer triangle
Encyclopedia
An integer triangle or integral triangle is a triangle
all of whose sides have lengths that are integers. A rational triangle can be defined as one having all sides with rational length; any such rational triangle can be integrally rescaled (can have all sides multiplied by the same integer, namely a common multiple of their denominators) to obtain an integer triangle, so there is no substantive difference between integer triangles and rational triangles in this sense. (Note however, that other definitions of the term "rational triangle" also exist: In 1914 Carmichael used the term in the sense that we today use the term Heronian triangle
; Somos uses it to refer to triangles whose ratios of sides are rational; Conway and Guy define a rational triangle as one with rational sides and rational angles measured in degrees—in which case the only rational triangle is the equilateral triangle.)
or Pythagorean triplet or Pythagorean triad. All Pythagorean triples with hypotenuse
with hypotenuse  which are primitive (the sides having no common factor) can be generated by
which are primitive (the sides having no common factor) can be generated by

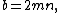
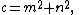
where m and n are coprime
integers and one of them is even with m > n.
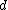 from the hypotenuse, which necessarily have both
from the hypotenuse, which necessarily have both 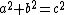 and
and 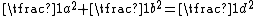 , are generated by
, are generated by
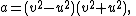
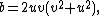

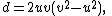
for coprime integers u, v with v > u.
Furthermore, any Pythagorean triangle with legs x, y and hypotenuse z can generate another Pythagorean triangle, this one with integer altitude d from the hypotenuse c, by
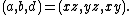
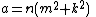

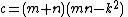
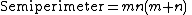
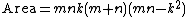
for integers m, n and k subject to the contraints:
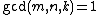
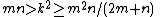
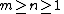 .
.
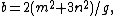
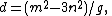
and where g is the greatest common divisor of
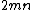 , and
, and 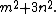
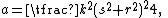
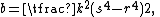
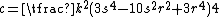
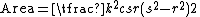
with integers k, s, r such that s2 > 3r2, or
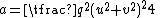 ,
,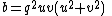 ,
,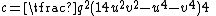 ,
, ,
,
with integers q, u, v such that v > u and v2 < (7+4√3)u2.
No triangles with B = 2A are Pythagorean.
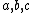 and with rational bisector
and with rational bisector  of angle A is given by
of angle A is given by
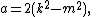
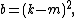
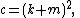
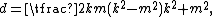
with integers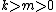 .
.
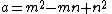
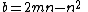
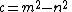
with coprime integers m, n with 0 < n < m (the angle of 60° is opposite to the side of length a). From here, all primitive solutions can be obtained by dividing a, b, and c by their greatest common divisor (e.g. an equilateral triangle solution is obtained by taking m = 2 and n = 1, but this produces a = b = c = 3, which is not a primitive solution). See also
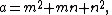
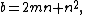
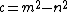
with coprime integers m, n with 0 < n < m (the angle of 120° is opposite to the side of length a). From here, all primitive solutions can be obtained by dividing a, b, and c by their greatest common divisor (e.g. by taking m = 4 and n = 1, one obtains a = 21, b = 9 and c = 15, which is not a primitive solution, but leads to the primitive solution a = 7, b = 3, and c = 5 which, up to order, can be obtained with the values m = 2 and n = 1). See also.
 and angle B opposite side
and angle B opposite side 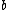 , some triangles with B=2A are generated by
, some triangles with B=2A are generated by
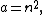

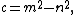
with integers m, n such that 0 < n < m < 2n.
Note that all triangles with B = 2A (whether integer or not) have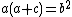 .
.
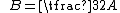 are generated by
are generated by
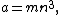
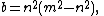

with integers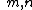 such that
such that 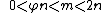 , where
, where  is the golden ratio
is the golden ratio
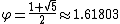 .
.
Note that all triangles with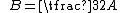 (whether with integer sides or not) satisfy
(whether with integer sides or not) satisfy 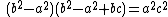 .
.
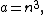
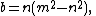
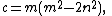
where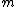 and
and  are integers such that
are integers such that 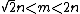 .
.
Note that all triangles with B = 3A (whether with integer sides or not) satisfy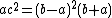 .
.
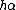 ,
, 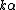 , and
, and 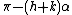 and hence two angles in the ratio h : k, and its sides are integers:
and hence two angles in the ratio h : k, and its sides are integers:
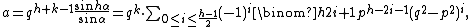
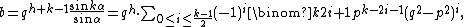
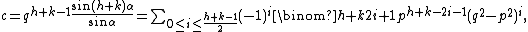
where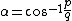 and p and q are any relatively prime integers such that
and p and q are any relatively prime integers such that  .
.
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
all of whose sides have lengths that are integers. A rational triangle can be defined as one having all sides with rational length; any such rational triangle can be integrally rescaled (can have all sides multiplied by the same integer, namely a common multiple of their denominators) to obtain an integer triangle, so there is no substantive difference between integer triangles and rational triangles in this sense. (Note however, that other definitions of the term "rational triangle" also exist: In 1914 Carmichael used the term in the sense that we today use the term Heronian triangle
Heronian triangle
In geometry, a Heronian triangle is a triangle whose sidelengths and area are all rational numbers. It is named after Hero of Alexandria. Any such rational triangle can be scaled up to a corresponding triangle with integer sides and area, and often the term Heronian triangle is used to refer to...
; Somos uses it to refer to triangles whose ratios of sides are rational; Conway and Guy define a rational triangle as one with rational sides and rational angles measured in degrees—in which case the only rational triangle is the equilateral triangle.)
Pythagorean triangles
A Pythagorean triangle has a right angle and three integer sides, which are known as a Pythagorean triplePythagorean triple
A Pythagorean triple consists of three positive integers a, b, and c, such that . Such a triple is commonly written , and a well-known example is . If is a Pythagorean triple, then so is for any positive integer k. A primitive Pythagorean triple is one in which a, b and c are pairwise coprime...
or Pythagorean triplet or Pythagorean triad. All Pythagorean triples
 with hypotenuse
with hypotenuse  which are primitive (the sides having no common factor) can be generated by
which are primitive (the sides having no common factor) can be generated by
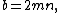
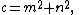
where m and n are coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
integers and one of them is even with m > n.
Pythagorean triangles with integer altitude from the hypotenuse
All primitive Pythagorean triangles with legs a b, hypotenuse c, and integer altitude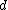 from the hypotenuse, which necessarily have both
from the hypotenuse, which necessarily have both 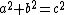 and
and 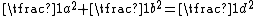 , are generated by
, are generated by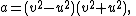
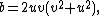

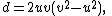
for coprime integers u, v with v > u.
Furthermore, any Pythagorean triangle with legs x, y and hypotenuse z can generate another Pythagorean triangle, this one with integer altitude d from the hypotenuse c, by
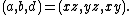
Heronian triangles
A Heronian triangle, also known as a Heron triangle or a Hero triangle, is a triangle with integer sides and integer area. All Heronian triangles can be generated as multiples of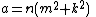

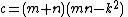
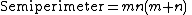
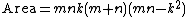
for integers m, n and k subject to the contraints:
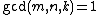
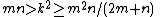
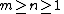 .
.Heronian triangles with sides in arithmetic progression
A triangle with integer sides and integer area has sides in arithmetic progression if and only if the sides are (b – d, b, b + d), where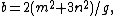
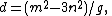
and where g is the greatest common divisor of

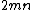 , and
, and 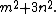
Heronian triangles with one angle equal to twice another
All Heronian triangles with B=2A are generated by either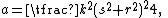
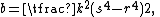
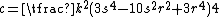
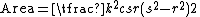
with integers k, s, r such that s2 > 3r2, or
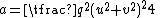 ,
,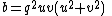 ,
,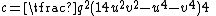 ,
, ,
,with integers q, u, v such that v > u and v2 < (7+4√3)u2.
No triangles with B = 2A are Pythagorean.
Integer triangles with a rational angle bisector
A triangle family with integer sides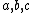 and with rational bisector
and with rational bisector  of angle A is given by
of angle A is given by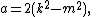
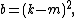
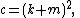
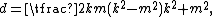
with integers
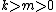 .
.Integer triangles with a 60° angle
Integer triangles with a 60° angle can be generated by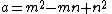
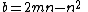
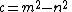
with coprime integers m, n with 0 < n < m (the angle of 60° is opposite to the side of length a). From here, all primitive solutions can be obtained by dividing a, b, and c by their greatest common divisor (e.g. an equilateral triangle solution is obtained by taking m = 2 and n = 1, but this produces a = b = c = 3, which is not a primitive solution). See also
Integer triangles with a 120° angle
Integer triangles with a 120° angle can be generated by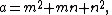
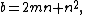
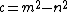
with coprime integers m, n with 0 < n < m (the angle of 120° is opposite to the side of length a). From here, all primitive solutions can be obtained by dividing a, b, and c by their greatest common divisor (e.g. by taking m = 4 and n = 1, one obtains a = 21, b = 9 and c = 15, which is not a primitive solution, but leads to the primitive solution a = 7, b = 3, and c = 5 which, up to order, can be obtained with the values m = 2 and n = 1). See also.
Integer triangles with one angle equal to twice another
With angle A opposite side and angle B opposite side
and angle B opposite side 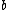 , some triangles with B=2A are generated by
, some triangles with B=2A are generated by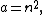

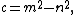
with integers m, n such that 0 < n < m < 2n.
Note that all triangles with B = 2A (whether integer or not) have
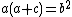 .
.Integer triangles with one angle equal to 3/2 times another
The equivalence class of similar triangles with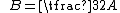 are generated by
are generated by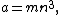
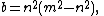

with integers
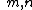 such that
such that 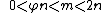 , where
, where  is the golden ratio
is the golden ratioGolden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
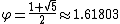 .
.Note that all triangles with
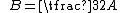 (whether with integer sides or not) satisfy
(whether with integer sides or not) satisfy 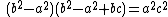 .
.Integer triangles with one angle three times another
We can generate the full equivalence class of similar triangles that satisfy B=3A by using the formulas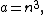
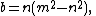
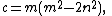
where
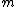 and
and  are integers such that
are integers such that 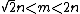 .
.Note that all triangles with B = 3A (whether with integer sides or not) satisfy
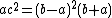 .
.Integer triangles with one angle equal to an arbitrary rational number times another angle
For positive relatively prime integers h and k, the triangle with the following sides has angles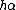 ,
, 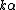 , and
, and 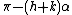 and hence two angles in the ratio h : k, and its sides are integers:
and hence two angles in the ratio h : k, and its sides are integers: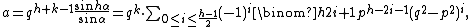
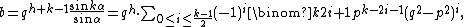
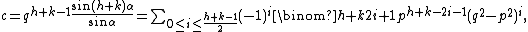
where
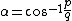 and p and q are any relatively prime integers such that
and p and q are any relatively prime integers such that  .
.Properties
- The only triangle with consecutive integers for sides and area has sides
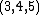 and area
and area  .
.
- The only triangle with consecutive integers for an altitude and the sides has sides
 and altitude from side 14 equal to 12.
and altitude from side 14 equal to 12.
- The
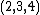 triangle and its multiples are the only triangles with integer sides in arithmetic progression and having the complementary exterior angle property. This property states that if angle C is obtuse and if a segment is dropped from B meeting perpendicularly AC extended at P, then ∠CAB=2∠CBP.
triangle and its multiples are the only triangles with integer sides in arithmetic progression and having the complementary exterior angle property. This property states that if angle C is obtuse and if a segment is dropped from B meeting perpendicularly AC extended at P, then ∠CAB=2∠CBP.
- The
 triangle and its multiples are the only integer right triangles having sides in arithmetic progression
triangle and its multiples are the only integer right triangles having sides in arithmetic progression
- The
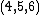 triangle and its multiples are the only triangles with one angle being twice another and having integer sides in arithmetic progression.
triangle and its multiples are the only triangles with one angle being twice another and having integer sides in arithmetic progression.
- The
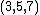 triangle and its multiples are the only triangles with a 120° angle and having integer sides in arithmetic progression.
triangle and its multiples are the only triangles with a 120° angle and having integer sides in arithmetic progression.
- The only integer triangle with area=semiperimeter has sides
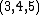 .
.
- The only integer triangles with area = perimeter have sides (5, 12, 13), (6,8,10), (6,25,29), (7,15,20), and (9,10,17). Of these the first two, but not the last three, are right triangles.
- The perimeter of a Heron triangle is always an even number.
- The area of a Heron triangle is always divisible by 6.
- There are no equilateral Heronian triangles.
- There are no Heronian triangles whose side lengths form a geometric progressionGeometric progressionIn mathematics, a geometric progression, also known as a geometric sequence, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed non-zero number called the common ratio. For example, the sequence 2, 6, 18, 54, ... is a geometric progression...
.
- There exist integer triangles with three rational mediansMedian (geometry)In geometry, a median of a triangle is a line segment joining a vertex to the midpoint of the opposing side. Every triangle has exactly three medians; one running from each vertex to the opposite side...
. The smallest has sides (68, 85, 87). Others include (127, 131, 158) and (204, 255, 261).

