
Integral nonlinearity
Encyclopedia
Integral nonlinearity is a term describing the maximum deviation between the ideal output of a DAC and the actual output level (after offset and gain errors have been removed). The term is often used as an important specification for measuring error in a digital-to-analog converter (DAC).
The transfer function of a DAC should ideally be a line and the INL measurement depends on the line selected. Two often used lines are the best fit line, which is the line that minimizes the INL result and the endpoint line which is a line that passes through the points on the transfer function corresponding to the lowest and highest input code. In all cases, the INL is the maximum distance between the ideal line selected and the actual transfer function.
is
where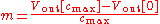
is the slope of the line through the end points, and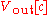
is the output voltage at code c. This assumes that the minimum code is 0. This INL is measured in volts; one can divide it by the ideal LSB voltage to get the measurement in LSBs.
The transfer function of a DAC should ideally be a line and the INL measurement depends on the line selected. Two often used lines are the best fit line, which is the line that minimizes the INL result and the endpoint line which is a line that passes through the points on the transfer function corresponding to the lowest and highest input code. In all cases, the INL is the maximum distance between the ideal line selected and the actual transfer function.
Formula
For the line through the endpoints, the INL of a DACDigital-to-analog converter
In electronics, a digital-to-analog converter is a device that converts a digital code to an analog signal . An analog-to-digital converter performs the reverse operation...
is

where
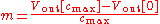
is the slope of the line through the end points, and
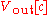
is the output voltage at code c. This assumes that the minimum code is 0. This INL is measured in volts; one can divide it by the ideal LSB voltage to get the measurement in LSBs.
External links
- INL/DNL Measurements for High-Speed Analog-to-Digital Converters (ADCs) Application Note 283 by Maxim

