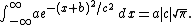Integral of a Gaussian function
Encyclopedia
The integral of an arbitrary Gaussian function is

An alternative form is
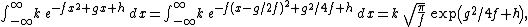
where f must be strictly positive for the integral to converge.
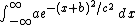
can be calculated by putting it into the form of a Gaussian integral
. First, the constant a can simply be factored out of the integral. Next, the variable of integration is changed from x to y = x + b.
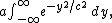
and then to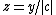
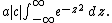
Then, using the Gaussian integral identity
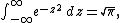
we have
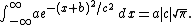

An alternative form is
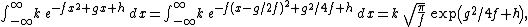
where f must be strictly positive for the integral to converge.
Proof
The integral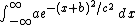
can be calculated by putting it into the form of a Gaussian integral
Gaussian integral
The Gaussian integral, also known as the Euler-Poisson integral or Poisson integral, is the integral of the Gaussian function e−x2 over the entire real line.It is named after the German mathematician and...
. First, the constant a can simply be factored out of the integral. Next, the variable of integration is changed from x to y = x + b.
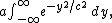
and then to
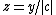
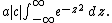
Then, using the Gaussian integral identity
Gaussian integral
The Gaussian integral, also known as the Euler-Poisson integral or Poisson integral, is the integral of the Gaussian function e−x2 over the entire real line.It is named after the German mathematician and...
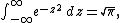
we have