Integrodifference equation
Encyclopedia
In mathematics
, an integrodifference equation is a recurrence relation
on a function space
, of the following form:
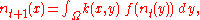
where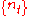
is a sequence in the function space and 
is the domain of those functions. In most applications, for any 
, 
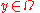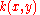is a probability density function
on
. Note that in the definition above, 
can be vector valued, in which case each element of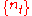 
has a scalar valued integrodifference equation associated with it. Integrodifference equations are widely used in mathematical biology
, especially theoretical ecology
, to model the dispersal
and growth of populations. In this case,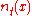
is the population size or density at location 
at time 
, 
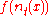describes the local population growth at location 
and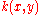 
, is the probability of moving from point 
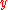to point 
, often referred to as the dispersal kernel. Integrodifference equations are most commonly used to describe univoltine
populations, including, but not limited to, many arthropod, and annual plant species. However, multivoltine populations can also be modeled with integrodifference equations, as long as the organism has non-overlapping generations. In this case,
is not measured in years, but rather the time increment between broods.
written as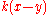
. In this case, some natural conditions on f and k imply that there is a well-defined
spreading speed for waves of invasion generated from compact initial conditions. The wave speed is often calculated
by studying the linearized equation
where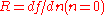
.
This can be written as the convoluion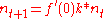
Using a moment-generating-function transformation
it has been shown that the critical wave speed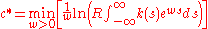
Other types of equations used to model population dynamics through space include reaction-diffusion equations and metapopulation
equations. However, diffusion equations do not as easily allow for the inclusion of explicit dispersal patterns and are only biologically accurate for populations with overlapping generations. Metapopulation equations are different from integrodifference equations in the fact that they break the population down into discrete patches rather than a continuous landscape.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an integrodifference equation is a recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
on a function space
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
, of the following form:
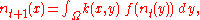
where
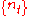is a sequence in the function space and is the domain of those functions. In most applications, for any 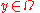, 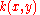is a probability density functionProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
on
. Note that in the definition above, can be vector valued, in which case each element of 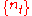has a scalar valued integrodifference equation associated with it. Integrodifference equations are widely used in mathematical biologyMathematical biology
Mathematical and theoretical biology is an interdisciplinary scientific research field with a range of applications in biology, medicine and biotechnology...
, especially theoretical ecology
Theoretical ecology
Theoretical ecology is the scientific discipline devoted to the study of ecological systems using theoretical methods such as simple conceptual models, mathematical models, computational simulations, and advanced data analysis...
, to model the dispersal
Biological dispersal
Biological dispersal refers to species movement away from an existing population or away from the parent organism. Through simply moving from one habitat patch to another, the dispersal of an individual has consequences not only for individual fitness, but also for population dynamics, population...
and growth of populations. In this case,
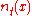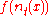is the population size or density at location at time , describes the local population growth at location and 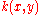, is the probability of moving from point 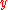to point , often referred to as the dispersal kernel. Integrodifference equations are most commonly used to describe univoltineVoltinism
Voltinism is a term used in biology to indicate the number of broods or generations of an organism in a year. The term is particularly in use in sericulture, where silkworm varieties vary in their voltinism....
populations, including, but not limited to, many arthropod, and annual plant species. However, multivoltine populations can also be modeled with integrodifference equations, as long as the organism has non-overlapping generations. In this case,
is not measured in years, but rather the time increment between broods.Convolution Kernels and Invasion Speeds
In one spatial dimension, the dispersal kernel often depends only on the distance between the source and the destination, and can bewritten as
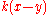. In this case, some natural conditions on f and k imply that there is a well-definedspreading speed for waves of invasion generated from compact initial conditions. The wave speed is often calculated
by studying the linearized equation
where
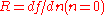.This can be written as the convoluion
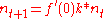
Using a moment-generating-function transformation
it has been shown that the critical wave speed
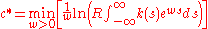
Other types of equations used to model population dynamics through space include reaction-diffusion equations and metapopulation
Metapopulation
A metapopulation consists of a group of spatially separated populations of the same species which interact at some level. The term metapopulation was coined by Richard Levins in 1970 to describe a model of population dynamics of insect pests in agricultural fields, but the idea has been most...
equations. However, diffusion equations do not as easily allow for the inclusion of explicit dispersal patterns and are only biologically accurate for populations with overlapping generations. Metapopulation equations are different from integrodifference equations in the fact that they break the population down into discrete patches rather than a continuous landscape.