Intersection theorem
Encyclopedia
In projective geometry
, an intersection theorem or incidence theorem is an incidence structure
consisting of points, lines, and possibly higher-dimensional objects and their incidences, together with a pair of nonincident objects A and B (for instance, a point and a line). The "theorem
" states that, whenever a set of objects satisfies the incidences (i.e. can be matched up with the objects of the incidence structure in a way that preserves incidence), then the objects corresponding to A and B must also be incident. An intersection theorem is not necessarily true in all projective geometries; it is rather a property which some geometries satisfy but not others.
For example, Desargues' theorem
can be stated using the following incidence structure:
The implication is then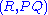
—that point R is incident with line PQ.
holds in a projective plane P if and only if
P is the projective plane over some division ring
D—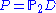
. The projective plane is then called desarguesian
.
A theorem of Amitsur
and Bergman states that, in the context of desarguesian projective planes, for every intersection theorem there is a rational identity such that the plane P satisfies the intersection theorem if and only if the division ring D satisfies the rational identity.
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
, an intersection theorem or incidence theorem is an incidence structure
Incidence structure
In mathematics, an incidence structure is a tripleC=.\,where P is a set of "points", L is a set of "lines" and I \subseteq P \times L is the incidence relation. The elements of I are called flags. If \in I,...
consisting of points, lines, and possibly higher-dimensional objects and their incidences, together with a pair of nonincident objects A and B (for instance, a point and a line). The "theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
" states that, whenever a set of objects satisfies the incidences (i.e. can be matched up with the objects of the incidence structure in a way that preserves incidence), then the objects corresponding to A and B must also be incident. An intersection theorem is not necessarily true in all projective geometries; it is rather a property which some geometries satisfy but not others.
For example, Desargues' theorem
Desargues' theorem
In projective geometry, Desargues' theorem, named in honor of Gérard Desargues, states:Denote the three vertices of one triangle by a, b, and c, and those of the other by A, B, and C...
can be stated using the following incidence structure:
- Points:
- Lines:
- Incidences (in addition to obvious ones such as
: 
The implication is then
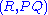—that point R is incident with line PQ.Famous examples
Desargues' theoremDesargues' theorem
In projective geometry, Desargues' theorem, named in honor of Gérard Desargues, states:Denote the three vertices of one triangle by a, b, and c, and those of the other by A, B, and C...
holds in a projective plane P if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
P is the projective plane over some division ring
Division ring
In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
D—
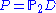. The projective plane is then called desarguesianDesarguesian plane
In projective geometry a Desarguesian plane, named after Gérard Desargues, is a plane in which Desargues' theorem holds. The ordinary real projective plane is a Desarguesian plane. More generally any projective plane over a division ring is Desarguesian, and conversely Hilbert showed that any...
.
A theorem of Amitsur
Shimshon Amitsur
Shimshon Avraham Amitsur was a Jewish mathematician. He is best known for his work in ring theory, in particular PI rings, an area of abstract algebra.-Biography:...
and Bergman states that, in the context of desarguesian projective planes, for every intersection theorem there is a rational identity such that the plane P satisfies the intersection theorem if and only if the division ring D satisfies the rational identity.
- Pappus's hexagon theoremPappus's hexagon theoremIn mathematics, Pappus's hexagon theorem states that given one set of collinear points A, B, C, and another set of collinear points a, b, c, then the intersection points X, Y, Z of line pairs Ab and aB, Ac and aC, Bc and bC are collinear...
holds in a desarguesian projective plane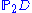
if and only if D is a fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
; it corresponds to the identity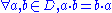
. - Fano's theorem (which states a certain intersection does not happen) holds in
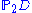if and only if D has characteristicCharacteristic (algebra)In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
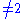; it corresponds to the identity a+a=0.