
Invariance theorem
Encyclopedia
In algorithmic information theory
, the invariance theorem, originally proved by Ray Solomonoff
, states that a universal Turing machine
provides an optimal means of description, up to an additive constant. Formally, for every machine M there exists a constant c such that for all binary strings x we have
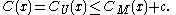
This follows trivially from the definition of a universal Turing machine
, taking c = ℓ (<M>) as the length of the encoding of M.
The invariance theorem holds likewise for prefix and conditional complexities.
Algorithmic information theory
Algorithmic information theory is a subfield of information theory and computer science that concerns itself with the relationship between computation and information...
, the invariance theorem, originally proved by Ray Solomonoff
Ray Solomonoff
Ray Solomonoff was the inventor of algorithmic probability, and founder of algorithmic information theory, He was an originator of the branch of artificial intelligence based on machine learning, prediction and probability...
, states that a universal Turing machine
Universal Turing machine
In computer science, a universal Turing machine is a Turing machine that can simulate an arbitrary Turing machine on arbitrary input. The universal machine essentially achieves this by reading both the description of the machine to be simulated as well as the input thereof from its own tape. Alan...
provides an optimal means of description, up to an additive constant. Formally, for every machine M there exists a constant c such that for all binary strings x we have
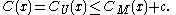
This follows trivially from the definition of a universal Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
, taking c = ℓ (<M>) as the length of the encoding of M.
The invariance theorem holds likewise for prefix and conditional complexities.

