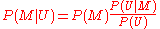Inverse gambler's fallacy
Encyclopedia
The inverse gambler's fallacy, named by philosopher Ian Hacking
, is a formal fallacy
of Bayesian inference
which is similar to the better known gambler's fallacy
. It is the fallacy of concluding, on the basis of an unlikely outcome of a random process, that the process is likely to have occurred many times before. For example, if one observes a pair of fair dice
being rolled and turning up double sixes, it is wrong to suppose that this lends any support to the hypothesis that the dice have been rolled before. We can see this from the Bayesian update rule: letting U denote the unlikely outcome of the random process and M the proposition that the process has occurred before, we have
and since P(U|M) = P(U) (the outcome of the process is unaffected by previous occurrences), it follows that P(M|U) = P(M); that is, our confidence in M should be unchanged when we learn U.
to support life, and second, that this fine tuning points to the existence of an intelligent designer. The rebuttal attacked by Hacking consists of accepting the first premise, but rejecting the second on the grounds that our (big bang) universe is just one in a long sequence of universes, and that the fine tuning merely shows that there have been many other (poorly tuned) universes preceding this one. Hacking draws a sharp distinction between this argument and the argument that all possible worlds coexist in some non-temporal sense. He proposes that these arguments, often treated as minor variations of one another, should be considered fundamentally different because one is formally invalid while the other is not.
A rebuttal paper by John Leslie
points out a difference between the observation of double sixes and the observation of fine tuning, namely that the former is not necessary (the roll could have come out differently) while the latter is necessary (our universe must support life
, which means ex hypothesi that we must see fine tuning). He suggests the following analogy: instead of being summoned into a room to observe a particular roll of the dice, we are told that we will be summoned into the room immediately after a roll of double sixes. In this situation it may be quite reasonable, upon being summoned, to conclude with high confidence that we are not seeing the first roll. In particular, if we know that the dice are fair and that the rolling would not have been stopped before double sixes turned up, then the probability that we are seeing the first roll is at most 1/36. (It may be smaller because we have not assumed that the roller is obliged to summon us the first time double sixes come up.)
Suppose a man walked into a room and saw someone rolling a pair of dice. Furthermore, imagine that the result of this dice roll is a double-six. The man entering the room would commit the Inverse Gambler's Fallacy if he said, "You've probably been rolling the dice for quite a while, since it's unlikely you would get a double-six on your first attempt."
Ian Hacking
Ian Hacking, CC, FRSC, FBA is a Canadian philosopher, specializing in the philosophy of science.- Life and works :...
, is a formal fallacy
Formal fallacy
In philosophy, a formal fallacy is a pattern of reasoning that is always wrong. This is due to a flaw in the logical structure of the argument which renders the argument invalid...
of Bayesian inference
Bayesian inference
In statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...
which is similar to the better known gambler's fallacy
Gambler's fallacy
The Gambler's fallacy, also known as the Monte Carlo fallacy , and also referred to as the fallacy of the maturity of chances, is the belief that if deviations from expected behaviour are observed in repeated independent trials of some random process, future deviations in the opposite direction are...
. It is the fallacy of concluding, on the basis of an unlikely outcome of a random process, that the process is likely to have occurred many times before. For example, if one observes a pair of fair dice
Dice
A die is a small throwable object with multiple resting positions, used for generating random numbers...
being rolled and turning up double sixes, it is wrong to suppose that this lends any support to the hypothesis that the dice have been rolled before. We can see this from the Bayesian update rule: letting U denote the unlikely outcome of the random process and M the proposition that the process has occurred before, we have
and since P(U|M) = P(U) (the outcome of the process is unaffected by previous occurrences), it follows that P(M|U) = P(M); that is, our confidence in M should be unchanged when we learn U.
Real-world examples
The inverse gambler's fallacy is unquestionably a fallacy, but there is disagreement over whether and where it has been committed in practice. In his original paper, Hacking takes as his main example a certain response to the argument from design. The argument from design asserts, first, that the universe is fine tunedFine-tuned universe
The fine-tuned universe is the proposition that the conditions that allow life in the Universe can only occur when certain universal fundamental physical constants lie within a very narrow range, so that if any of several fundamental constants were only slightly different the universe would be...
to support life, and second, that this fine tuning points to the existence of an intelligent designer. The rebuttal attacked by Hacking consists of accepting the first premise, but rejecting the second on the grounds that our (big bang) universe is just one in a long sequence of universes, and that the fine tuning merely shows that there have been many other (poorly tuned) universes preceding this one. Hacking draws a sharp distinction between this argument and the argument that all possible worlds coexist in some non-temporal sense. He proposes that these arguments, often treated as minor variations of one another, should be considered fundamentally different because one is formally invalid while the other is not.
A rebuttal paper by John Leslie
John A. Leslie
John Andrew Leslie is a Canadian philosopher. He was educated at Wadham College, Oxford, earning his B.A. in English Literature in 1962 and his M.Litt. in Classics in 1968...
points out a difference between the observation of double sixes and the observation of fine tuning, namely that the former is not necessary (the roll could have come out differently) while the latter is necessary (our universe must support life
Anthropic principle
In astrophysics and cosmology, the anthropic principle is the philosophical argument that observations of the physical Universe must be compatible with the conscious life that observes it. Some proponents of the argument reason that it explains why the Universe has the age and the fundamental...
, which means ex hypothesi that we must see fine tuning). He suggests the following analogy: instead of being summoned into a room to observe a particular roll of the dice, we are told that we will be summoned into the room immediately after a roll of double sixes. In this situation it may be quite reasonable, upon being summoned, to conclude with high confidence that we are not seeing the first roll. In particular, if we know that the dice are fair and that the rolling would not have been stopped before double sixes turned up, then the probability that we are seeing the first roll is at most 1/36. (It may be smaller because we have not assumed that the roller is obliged to summon us the first time double sixes come up.)
Suppose a man walked into a room and saw someone rolling a pair of dice. Furthermore, imagine that the result of this dice roll is a double-six. The man entering the room would commit the Inverse Gambler's Fallacy if he said, "You've probably been rolling the dice for quite a while, since it's unlikely you would get a double-six on your first attempt."