The inverse

Inverse function

In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...

s of the hyperbolic function

Hyperbolic function

In mathematics, hyperbolic functions are analogs of the ordinary trigonometric, or circular, functions. The basic hyperbolic functions are the hyperbolic sine "sinh" , and the hyperbolic cosine "cosh" , from which are derived the hyperbolic tangent "tanh" and so on.Just as the points form a...

s are the area hyperbolic functions. The names hint at the fact that they give the area of a sector of the unit hyperbola  in the same way that the inverse trigonometric function

Inverse trigonometric function

In mathematics, the inverse trigonometric functions are the inverse functions of the trigonometric functions with suitably restricted domains .The notations sin−1, cos−1, etc...

s give the arc length of a sector on the unit circle . The abbreviations arcsinh, arccosh, etc., are commonly used, even though they are misnomers, since the prefix arc is the abbreviation for arcus, while the prefix ar stands for area.Other authors prefer to use the notation argsinh, argcosh, argtanh, and so on. In computer science this is often shortened to asinh. The notation sinh⁻¹(x), cosh⁻¹(x), etc., is also used, despite the fact that care must be taken to avoid misinterpretations of the superscript −1 as a power as opposed to a shorthand for inverse (e.g., cosh⁻¹(x) versus cosh(x)⁻¹).

The values of inverse hyperbolic functions are hyperbolic angle

Hyperbolic angle

In mathematics, a hyperbolic angle is a geometric figure that divides a hyperbola. The science of hyperbolic angle parallels the relation of an ordinary angle to a circle...

s.

Logarithmic representation

The operators are defined in the complex plane by: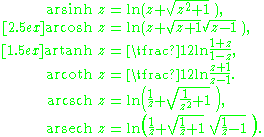


The above square roots are principal square root

Square root

In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...

s, and the logarithm function is the complex logarithm. For real arguments, i.e., z = x, which return real values, certain simplifications can be made e.g. 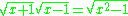, which are not generally true when using principal square roots.

Inverse hyperbolic functions in the complex plane

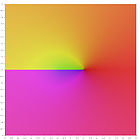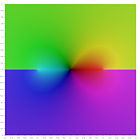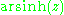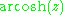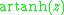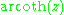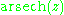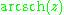Series expansions

Expansion series can be obtained for the above functions: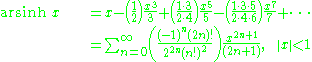






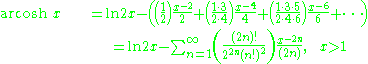
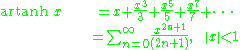
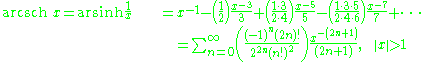
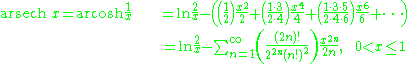
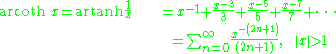
Asymptotic expansion for the arsinh x is given by

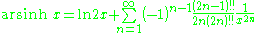
Derivatives

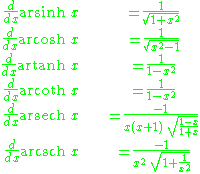
For real x:


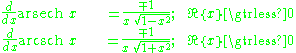
For an example differentiation: let θ = arsinh x, so:

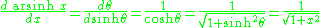
Composition of hyperbolic and inverse hyperbolic functions

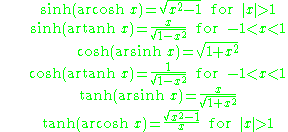
Addition formulae

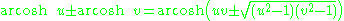
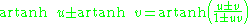
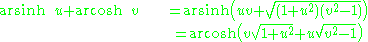
External links

• Inverse hyperbolic functions at MathWorld
  MathWorld
  MathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...
  
  
• Inverse hyperbolic functions at University College London Department of Mathematics