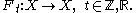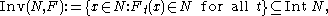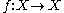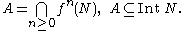Isolating neighborhood
Encyclopedia
In the theory of dynamical systems, an isolating neighborhood is a compact set in the phase space
of an invertible dynamical system with the property that any orbit contained entirely in the set belongs to its interior
. This is a basic notion in the Conley index theory. Its variant for non-invertible systems is used in formulating a precise mathematical definition of an attractor
.
A compact subset N is called an isolating neighborhood if
where Int N is the interior of N. The set Inv(N,F) consists of all points whose trajectory remains in N for all positive and negative times. A set S is an isolated (or locally maximal) invariant set if S = Inv(N, F) for some isolating neighborhood N.
be a (non-invertible) discrete dynamical system. A compact invariant set A is called isolated, with (forward) isolating neighborhood N if A is the intersection of forward images of N and moreover, A is contained in the interior of N:
It is not assumed that the set N is either invariant or open.
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
of an invertible dynamical system with the property that any orbit contained entirely in the set belongs to its interior
Interior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
. This is a basic notion in the Conley index theory. Its variant for non-invertible systems is used in formulating a precise mathematical definition of an attractor
Attractor
An attractor is a set towards which a dynamical system evolves over time. That is, points that get close enough to the attractor remain close even if slightly disturbed...
.
Conley index theory
Let X be the phase space of an invertible discrete or continuous dynamical system with evolution operatorA compact subset N is called an isolating neighborhood if
where Int N is the interior of N. The set Inv(N,F) consists of all points whose trajectory remains in N for all positive and negative times. A set S is an isolated (or locally maximal) invariant set if S = Inv(N, F) for some isolating neighborhood N.
Milnor's definition of attractor
Letbe a (non-invertible) discrete dynamical system. A compact invariant set A is called isolated, with (forward) isolating neighborhood N if A is the intersection of forward images of N and moreover, A is contained in the interior of N:
It is not assumed that the set N is either invariant or open.