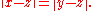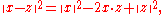Isosceles triangle theorem
Encyclopedia
In Euclidean geometry
, the isosceles triangle theorem, also known as the pons asinorum, states that the angles opposite the two equal sides of an isosceles triangle are equal. It is, in essence, the content of proposition 5 in Book I of Euclid's Elements
.
was one of the four subjects of the quadrivium
, this theorem acquired a reputation as an early yet difficult proposition and those who did not master its proof would be unable to go on to more advanced material. Perhaps because of this, the theorem became known as the pons asinorum or asses' bridge and is used as a metaphor for any early, difficult test.
points out, Euclid never uses the second conclusion and his proof can be simplified somewhat by drawing the auxiliary lines to the sides of the triangle instead, the rest of the proof proceeding in more or less the same way. There has been much speculation and debate as to why, given that it makes the proof more complicated, Euclid added the second conclusion to the theorem. One plausible explanation, given by Proclus, is that the second conclusion can be used in possible objections to the proofs of later propositions where Euclid does not cover every case. The proof relies heavily on what is today called side-angle-side, the previous proposition in the Elements.
Proclus' variation of Euclid's proof proceeds as follows:
Let ABC be an isosceles triangle with AB and AC being the equal sides. Pick an arbitrary point D on side AB and construct E on AC so that AD=AE. Draw the lines BE, DC and DE. Consider the triangles BAE and CAD; BA=CA, AE=AD, and angle A is equal to itself, so by side-angle-side, the triangles are congruent and corresponding sides and angles are equal. Therefore angle ABE = angle ACD, angle ADC = angle AEB, and BE=CD. Since AB=AC and AD=AE, BD=CE by subtraction of equal parts. Now consider the triangles DBE and ECD; BD=CE, BE=CD, and angle DBE = angle ECD have just been shown, so applying side-angle-side again, the triangles are congruent. Therefore angle BDE = angle CED and angle BED = angle CDE. (The congruence also implies DF = FD but this is self evident.) Since BDE = angle CED and angle CDE = BED, angle BDC = angle CEB by subtraction of equal parts. Consider a third pair of triangles, BDC and CEB; DB=EC, DC=EB, and angle BDC = angle CEB, so applying side-angle-side a third time, the triangles are congruent. In particular, angle CBD = BCE, which was to be proved.
. This is not only simpler but it requires no additional construction at all. The method of proof is to apply side-angle-side to the triangle and its mirror image. More modern authors, in imitation of the method of proof given for the previous proposition have described this as picking up the triangle, turning it over and laying it down upon itself.
This method is lampooned by Charles Dodgson in Euclid and his Modern Rivals
, calling it an "Irish bull
" because it apparently requires the triangle to be in two places at once.
The proof is as follows:
Let ABC be an isosceles triangle with AB and AC being the equal sides. Consider the triangles ABC and ACB, where ACB is considered a second triangle with vertices A, C and B corresponding respectively to A, B and C in the original triangle. AB=AC, AC=AB and angle A is equal to itself, so by side-angle-side, triangles ABC and ACB are congruent. In particular angle B = angle C.
This is simpler than Euclid's proof, but Euclid does not present the construction of an angle bisector until proposition 9. So the order of presentation of the Euclid's propositions would have to be changed to avoid the possibility of circular reasoning.
The proof proceeds as follows: As before, let the triangle be ABC with AB=AC. Construct the angle bisector of angle BAC and extend it to meet BC at X. AB=AC and AX is equal to itself. Furthermore angle BAX = angle CAX, so, applying side-angle-side, BAX and CAX are congruent. It follows that the angles at B and C are equal.
Legendre
uses a similar construction in Éléments de géométrie, but taking X to be the midpoint of BD. The proof is similar but side-side-side must be used instead of side-angle-side, and side-side-side is not given by Euclid until later in the Elements.
or complex number
s. In such spaces, it takes a form that says of vectors x, y, and z that if
then
Since
and
where θ is the angle between the two vectors, the conclusion of this inner product space form of the theorem is equivalent to the statement about equality of angles.
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, the isosceles triangle theorem, also known as the pons asinorum, states that the angles opposite the two equal sides of an isosceles triangle are equal. It is, in essence, the content of proposition 5 in Book I of Euclid's Elements
Euclid's Elements
Euclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...
.
Pons asinorum
In medieval times, when geometryGeometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
was one of the four subjects of the quadrivium
Quadrivium
The quadrivium comprised the four subjects, or arts, taught in medieval universities, after teaching the trivium. The word is Latin, meaning "the four ways" , and its use for the 4 subjects has been attributed to Boethius or Cassiodorus in the 6th century...
, this theorem acquired a reputation as an early yet difficult proposition and those who did not master its proof would be unable to go on to more advanced material. Perhaps because of this, the theorem became known as the pons asinorum or asses' bridge and is used as a metaphor for any early, difficult test.
Euclid and Proclus
Euclid's statement of the theorem includes a second conclusion that if the equal sides of the triangle are extended below the base, then the angles between the extensions and the base are also equal. Euclid's proof involves drawing auxiliary lines to these extensions. But, as Euclid's commentator ProclusProclus
Proclus Lycaeus , called "The Successor" or "Diadochos" , was a Greek Neoplatonist philosopher, one of the last major Classical philosophers . He set forth one of the most elaborate and fully developed systems of Neoplatonism...
points out, Euclid never uses the second conclusion and his proof can be simplified somewhat by drawing the auxiliary lines to the sides of the triangle instead, the rest of the proof proceeding in more or less the same way. There has been much speculation and debate as to why, given that it makes the proof more complicated, Euclid added the second conclusion to the theorem. One plausible explanation, given by Proclus, is that the second conclusion can be used in possible objections to the proofs of later propositions where Euclid does not cover every case. The proof relies heavily on what is today called side-angle-side, the previous proposition in the Elements.
Proclus' variation of Euclid's proof proceeds as follows:
Let ABC be an isosceles triangle with AB and AC being the equal sides. Pick an arbitrary point D on side AB and construct E on AC so that AD=AE. Draw the lines BE, DC and DE. Consider the triangles BAE and CAD; BA=CA, AE=AD, and angle A is equal to itself, so by side-angle-side, the triangles are congruent and corresponding sides and angles are equal. Therefore angle ABE = angle ACD, angle ADC = angle AEB, and BE=CD. Since AB=AC and AD=AE, BD=CE by subtraction of equal parts. Now consider the triangles DBE and ECD; BD=CE, BE=CD, and angle DBE = angle ECD have just been shown, so applying side-angle-side again, the triangles are congruent. Therefore angle BDE = angle CED and angle BED = angle CDE. (The congruence also implies DF = FD but this is self evident.) Since BDE = angle CED and angle CDE = BED, angle BDC = angle CEB by subtraction of equal parts. Consider a third pair of triangles, BDC and CEB; DB=EC, DC=EB, and angle BDC = angle CEB, so applying side-angle-side a third time, the triangles are congruent. In particular, angle CBD = BCE, which was to be proved.
Pappus
Proclus gives a much shorter proof attributed to Pappus of AlexandriaPappus of Alexandria
Pappus of Alexandria was one of the last great Greek mathematicians of Antiquity, known for his Synagoge or Collection , and for Pappus's Theorem in projective geometry...
. This is not only simpler but it requires no additional construction at all. The method of proof is to apply side-angle-side to the triangle and its mirror image. More modern authors, in imitation of the method of proof given for the previous proposition have described this as picking up the triangle, turning it over and laying it down upon itself.
This method is lampooned by Charles Dodgson in Euclid and his Modern Rivals
Euclid and his Modern Rivals
Euclid and his Modern Rivals is a mathematical book published in 1879 by the English mathematician Charles Lutwidge Dodgson , better known as Lewis Carroll...
, calling it an "Irish bull
Irish bull
An Irish bull is a ludicrous, incongruent or logically absurd statement, generally unrecognized as such by its author.The addition of the epithet Irish is a late addition....
" because it apparently requires the triangle to be in two places at once.
The proof is as follows:
Let ABC be an isosceles triangle with AB and AC being the equal sides. Consider the triangles ABC and ACB, where ACB is considered a second triangle with vertices A, C and B corresponding respectively to A, B and C in the original triangle. AB=AC, AC=AB and angle A is equal to itself, so by side-angle-side, triangles ABC and ACB are congruent. In particular angle B = angle C.
Others
A standard textbook method is to construct the bisector of the angle at A.This is simpler than Euclid's proof, but Euclid does not present the construction of an angle bisector until proposition 9. So the order of presentation of the Euclid's propositions would have to be changed to avoid the possibility of circular reasoning.
The proof proceeds as follows: As before, let the triangle be ABC with AB=AC. Construct the angle bisector of angle BAC and extend it to meet BC at X. AB=AC and AX is equal to itself. Furthermore angle BAX = angle CAX, so, applying side-angle-side, BAX and CAX are congruent. It follows that the angles at B and C are equal.
Legendre
Adrien-Marie Legendre
Adrien-Marie Legendre was a French mathematician.The Moon crater Legendre is named after him.- Life :...
uses a similar construction in Éléments de géométrie, but taking X to be the midpoint of BD. The proof is similar but side-side-side must be used instead of side-angle-side, and side-side-side is not given by Euclid until later in the Elements.
In inner product spaces
The isosceles triangle theorem holds in inner product spaces over the realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s. In such spaces, it takes a form that says of vectors x, y, and z that if
then
Since
and
where θ is the angle between the two vectors, the conclusion of this inner product space form of the theorem is equivalent to the statement about equality of angles.