Isotypic component
Encyclopedia
The Isotypic component of weight 
of a Lie algebra module is the sum of all submodules which are isomorphic to the highest weight module with weight 
.
This defines the isotypic component of weight
of V:
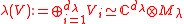where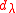 
is maximal.
of a Lie algebra module is the sum of all submodules which are isomorphic to the highest weight module with weight .Definition
- A finite dimensional moduleModule (mathematics)In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
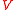of a reductive Lie algebra 
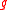(or of the correspondign Lie groupLie groupIn mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
) can be decomposed into irreducible submodules
. - Each finite dimensional irreducible representation of
is uniquely identified (up to isomorphism) by its highest weight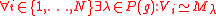
, where 
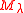denotes the highest weight module with highest weight 
. - In the decomposition of
, a certain isomorphism class might appear more than once, hence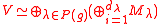
.
This defines the isotypic component of weight
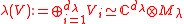of V: where 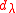is maximal.