Ito's lemma
Encyclopedia
In mathematics
, Itō
's lemma
is used in Itō stochastic calculus
to find the differential
of a function
of a particular type of stochastic process
. It is named after its discoverer, Kiyoshi Itō
. It is the stochastic calculus counterpart of the chain rule
in ordinary calculus
and is best memorized using the Taylor series expansion and retaining the second order term related to the stochastic component change. The lemma is widely employed in mathematical finance
and its best known application is in the derivation of the Black–Scholes equation used to value options. Ito's Lemma is also referred to currently as the Itō–Doeblin Theorem in recognition of the recently discovered work of Wolfgang Doeblin
.
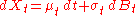
and any twice differentiable function ƒ(t, x) of two real variables t and x, one has
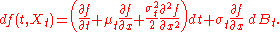
This immediately implies that ƒ(t, X) is itself an Itō drift-diffusion process.
In higher dimensions, Ito's lemma states
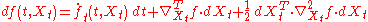
where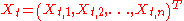
is a vector of Itō processes, 
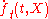is the partial differential w.r.t. t, 
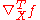is the gradient
of ƒ w.r.t. X, and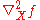
is the Hessian matrix
of ƒ w.r.t. X.
X = (X1,X2,…,Xd), and twice continuously differentiable and real valued function f on Rd. Some people prefer to present the formula in another form with cross variation shown explicitly as follows, f(X) is a semimartingale satisfying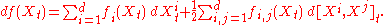
In this expression, the term fi represents the partial derivative
of f(x) with respect to xi, and [Xi,Xj ] is the quadratic covariation
process of Xi and Xj.
Let h be the jump intensity. The Poisson process
model for jumps is that the probability of one jump in the interval
is 
plus higher order terms. h could be a constant, a deterministic function of time, or a stochastic process. The survival probability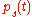 
is the probability that no jump has occurred in the interval 
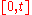. The change in the survival probability is
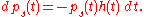
So
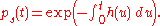
Let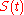
be a discontinuous stochastic process. Write 
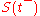for the value of S as we approach t from the left. Write 
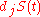for the non-infinitesimal change in 
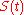as a result of a jump. Then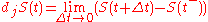
Let z be the magnitude of the jump and let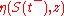
be the distribution
of z. The expected magnitude of the jump is
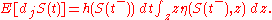
Define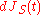
, a compensated process and martingale
, as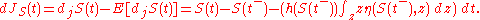
Then
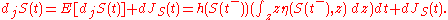
Consider a function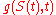
of jump process 
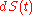. If 
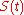jumps by 
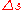then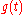 
jumps by 
. 
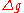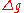is drawn from distribution 
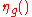which may depend on 
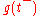, dg and 
. The jump part of 
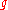is
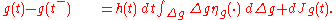
If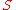
contains drift, diffusion and jump parts, then Itō's Lemma for 
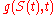is
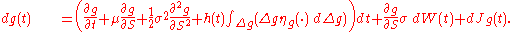
Itō's lemma for a process which is the sum of a drift-diffusion process and a jump process is just the sum of the Itō's lemma for the individual parts.
s, which need not be continuous. In general, a semimartingale is a càdlàg
process, and an additional term needs to be added to the formula to ensure that the jumps of the process are correctly given by Itō's lemma.
For any cadlag process Yt, the left limit in t is denoted by Yt-, which is a left-continuous process. The jumps are written as ΔYt = Yt - Yt-. Then, Itō's lemma states that if X = (X1,X2,…,Xd) is a d-dimensional semimartingale and f is a twice continuously differentiable real valued function on Rd then f(X) is a semimartingale, and
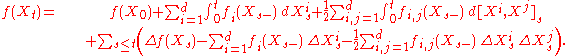
This differs from the formula for continuous semimartingales by the additional term summing over the jumps of X, which ensures that the jump of the right hand side at time t is Δf(Xt).
of the lemma requires us to take the limit of a sequence of random variables, which is not done here. Instead, we give a sketch of how one can derive Itō's lemma by expanding a Taylor series and applying the rules of stochastic calculus.
Assume the Itō process is in the form of
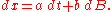
Expanding f(x, t) in a Taylor series
in x and t we have
and substituting a dt + b dB for dx gives
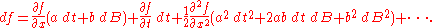
In the limit as dt tends to 0, the dt2 and dt dB terms disappear but the dB2 term tends to dt. The latter can be shown if we prove that
since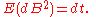 
Deleting the dt2 and dt dB terms, substituting dt for dB2, and collecting the dt and dB terms, we obtain
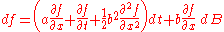
as required.
The formal proof is somewhat technical and is beyond the current state of this article.
with volatility σ and drift μ if it satisfies the stochastic differential equation
dS = S(σdB + μdt), for a Brownian motion B.
Applying Itō's lemma with f(S) = log(S) gives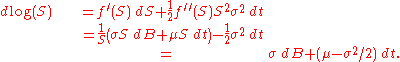
It follows that log(St) = log(S0) + σBt + (μ − σ2/2)t, and exponentiating gives the expression for S,
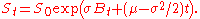
Applying Itō's lemma with f(Y) = log(Y) gives
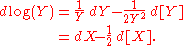
Exponentiating gives the solution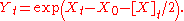
. Suppose a stock price follows a Geometric Brownian motion
given by the stochastic differential equation dS = S(σdB + μ dt).
Then, if the value of an option at time t is f(t,St), Itō's lemma gives
The term (∂f/∂S) dS represents the change in value in time dt of the trading strategy consisting of holding an amount ∂f/∂S of the stock. If this trading strategy is followed, and any cash held is assumed to grow at the risk free rate r, then the total value V of this portfolio satisfies the SDE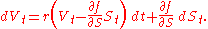
This strategy replicates the option if V = f(t,S).
Combining these equations gives the celebrated Black-Scholes equation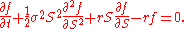
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Itō
Kiyoshi Ito
was a Japanese mathematician whose work is now called Itō calculus. The basic concept of this calculus is the Itō integral, and among the most important results is Itō's lemma. The Itō calculus facilitates mathematical understanding of random events...
's lemma
Lemma (mathematics)
In mathematics, a lemma is a proven proposition which is used as a stepping stone to a larger result rather than as a statement in-and-of itself...
is used in Itō stochastic calculus
Ito calculus
Itō calculus, named after Kiyoshi Itō, extends the methods of calculus to stochastic processes such as Brownian motion . It has important applications in mathematical finance and stochastic differential equations....
to find the differential
Differential (calculus)
In calculus, a differential is traditionally an infinitesimally small change in a variable. For example, if x is a variable, then a change in the value of x is often denoted Δx . The differential dx represents such a change, but is infinitely small...
of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of a particular type of stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
. It is named after its discoverer, Kiyoshi Itō
Kiyoshi Ito
was a Japanese mathematician whose work is now called Itō calculus. The basic concept of this calculus is the Itō integral, and among the most important results is Itō's lemma. The Itō calculus facilitates mathematical understanding of random events...
. It is the stochastic calculus counterpart of the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
in ordinary calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
and is best memorized using the Taylor series expansion and retaining the second order term related to the stochastic component change. The lemma is widely employed in mathematical finance
Mathematical finance
Mathematical finance is a field of applied mathematics, concerned with financial markets. The subject has a close relationship with the discipline of financial economics, which is concerned with much of the underlying theory. Generally, mathematical finance will derive and extend the mathematical...
and its best known application is in the derivation of the Black–Scholes equation used to value options. Ito's Lemma is also referred to currently as the Itō–Doeblin Theorem in recognition of the recently discovered work of Wolfgang Doeblin
Wolfgang Doeblin
Wolfgang Döblin, known in France as Vincent Doblin, was a German-French mathematician.-Life:Wolfgang was the son of the Jewish-German novelist, Alfred Döblin. His family escaped from Nazi Germany to France where he became a citizen...
.
Mathematical formulation of Itō's lemma
In the following subsections we discuss versions of Itō's lemma for different types of stochastic processes.Itō drift-diffusion processes
In its simplest form, Itō's lemma states the following: for an Itō drift-diffusion process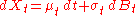and any twice differentiable function ƒ(t, x) of two real variables t and x, one has
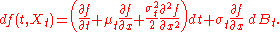
This immediately implies that ƒ(t, X) is itself an Itō drift-diffusion process.
In higher dimensions, Ito's lemma states
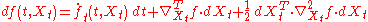
where
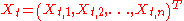is a vector of Itō processes, 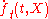is the partial differential w.r.t. t, 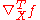is the gradientGradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of ƒ w.r.t. X, and
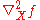is the Hessian matrixHessian matrix
In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
of ƒ w.r.t. X.
Continuous semimartingales
More generally, the above formula also holds for any continuous d-dimensional semimartingaleSemimartingale
In probability theory, a real valued process X is called a semimartingale if it can be decomposed as the sum of a local martingale and an adapted finite-variation process....
X = (X1,X2,…,Xd), and twice continuously differentiable and real valued function f on Rd. Some people prefer to present the formula in another form with cross variation shown explicitly as follows, f(X) is a semimartingale satisfying
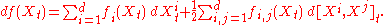
In this expression, the term fi represents the partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
of f(x) with respect to xi, and [Xi,Xj ] is the quadratic covariation
Quadratic variation
In mathematics, quadratic variation is used in the analysis of stochastic processes such as Brownian motion and martingales. Quadratic variation is just one kind of variation of a process.- Definition :...
process of Xi and Xj.
Poisson jump processes
We may also define functions on discontinuous stochastic processes.Let h be the jump intensity. The Poisson process
Poisson process
A Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...
model for jumps is that the probability of one jump in the interval
is plus higher order terms. h could be a constant, a deterministic function of time, or a stochastic process. The survival probability 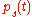is the probability that no jump has occurred in the interval 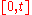. The change in the survival probability is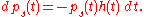So
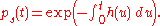
Let
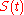be a discontinuous stochastic process. Write 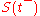for the value of S as we approach t from the left. Write 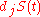for the non-infinitesimal change in 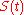as a result of a jump. Then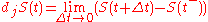Let z be the magnitude of the jump and let
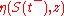be the distributionProbability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of z. The expected magnitude of the jump is
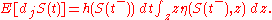
Define
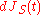, a compensated process and martingaleMartingale
Martingale can refer to:*Martingale , a stochastic process in which the conditional expectation of the next value, given the current and preceding values, is the current value*Martingale for horses...
, as
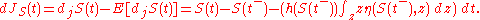
Then
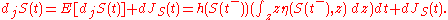
Consider a function
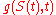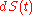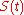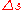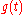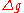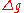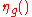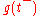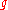of jump process . If jumps by then jumps by . is drawn from distribution which may depend on , dg and . The jump part of is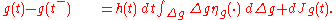If
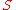contains drift, diffusion and jump parts, then Itō's Lemma for 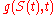is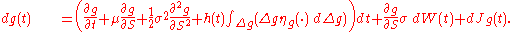Itō's lemma for a process which is the sum of a drift-diffusion process and a jump process is just the sum of the Itō's lemma for the individual parts.
Non-continuous semimartingales
Itō's lemma can also be applied to general d-dimensional semimartingaleSemimartingale
In probability theory, a real valued process X is called a semimartingale if it can be decomposed as the sum of a local martingale and an adapted finite-variation process....
s, which need not be continuous. In general, a semimartingale is a càdlàg
Càdlàg
In mathematics, a càdlàg , RCLL , or corlol function is a function defined on the real numbers that is everywhere right-continuous and has left limits everywhere...
process, and an additional term needs to be added to the formula to ensure that the jumps of the process are correctly given by Itō's lemma.
For any cadlag process Yt, the left limit in t is denoted by Yt-, which is a left-continuous process. The jumps are written as ΔYt = Yt - Yt-. Then, Itō's lemma states that if X = (X1,X2,…,Xd) is a d-dimensional semimartingale and f is a twice continuously differentiable real valued function on Rd then f(X) is a semimartingale, and
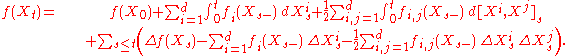
This differs from the formula for continuous semimartingales by the additional term summing over the jumps of X, which ensures that the jump of the right hand side at time t is Δf(Xt).
Informal derivation
A formal proofMathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
of the lemma requires us to take the limit of a sequence of random variables, which is not done here. Instead, we give a sketch of how one can derive Itō's lemma by expanding a Taylor series and applying the rules of stochastic calculus.
Assume the Itō process is in the form of
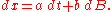
Expanding f(x, t) in a Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
in x and t we have
and substituting a dt + b dB for dx gives
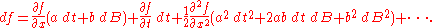
In the limit as dt tends to 0, the dt2 and dt dB terms disappear but the dB2 term tends to dt. The latter can be shown if we prove that
since 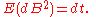Deleting the dt2 and dt dB terms, substituting dt for dB2, and collecting the dt and dB terms, we obtain
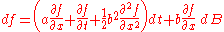
as required.
The formal proof is somewhat technical and is beyond the current state of this article.
Geometric Brownian motion
A process S is said to follow a geometric Brownian motionGeometric Brownian motion
A geometric Brownian motion is a continuous-time stochastic process in which the logarithm of the randomly varying quantity follows a Brownian motion, also called a Wiener process...
with volatility σ and drift μ if it satisfies the stochastic differential equation
Stochastic differential equation
A stochastic differential equation is a differential equation in which one or more of the terms is a stochastic process, thus resulting in a solution which is itself a stochastic process....
dS = S(σdB + μdt), for a Brownian motion B.
Applying Itō's lemma with f(S) = log(S) gives
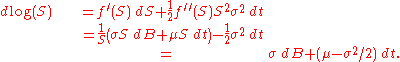
It follows that log(St) = log(S0) + σBt + (μ − σ2/2)t, and exponentiating gives the expression for S,
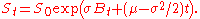
The Doléans exponential
The Doléans exponential (or stochastic exponential) of a continuous semimartingale X can be defined as the solution to the SDE dY = Y dX with initial condition Y0 = 1. It is sometimes denoted by (X).Applying Itō's lemma with f(Y) = log(Y) gives
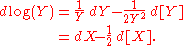
Exponentiating gives the solution
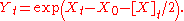
Black–Scholes formula
Itō's lemma can be used to derive the Black–Scholes formula for an optionOption (finance)
In finance, an option is a derivative financial instrument that specifies a contract between two parties for a future transaction on an asset at a reference price. The buyer of the option gains the right, but not the obligation, to engage in that transaction, while the seller incurs the...
. Suppose a stock price follows a Geometric Brownian motion
Geometric Brownian motion
A geometric Brownian motion is a continuous-time stochastic process in which the logarithm of the randomly varying quantity follows a Brownian motion, also called a Wiener process...
given by the stochastic differential equation dS = S(σdB + μ dt).
Then, if the value of an option at time t is f(t,St), Itō's lemma gives
The term (∂f/∂S) dS represents the change in value in time dt of the trading strategy consisting of holding an amount ∂f/∂S of the stock. If this trading strategy is followed, and any cash held is assumed to grow at the risk free rate r, then the total value V of this portfolio satisfies the SDE
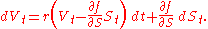
This strategy replicates the option if V = f(t,S).
Combining these equations gives the celebrated Black-Scholes equation
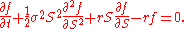
External links
- Derivation, Prof. Thayer Watkins
- Informal proof, optiontutor