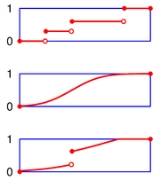
Càdlàg
Encyclopedia
In mathematics
, a càdlàg (French "continue à droite, limite à gauche"), RCLL (“right continuous with left limits”), or corlol (“continuous on (the) right, limit on (the) left”) function is a function defined on the real number
s (or a subset
of them) that is everywhere right-continuous
and has left limit
s everywhere. Càdlàg functions are important in the study of stochastic processes that admit (or even require) jumps, unlike Brownian motion
, which has continuous sample paths. The collection of càdlàg functions on a given domain is known as Skorokhod space.
Two related terms are càglàd, standing for "continue à gauche, limite à droite", the left-right reversal of càdlàg, and càllàl for"continue à l'un, limite à l’autre" (continuous on one side, limit on the other side), for a function which is interchangeably either càdlàg or càglàd at each point of the domain.
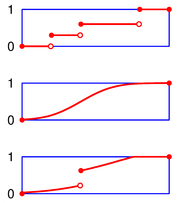 Let be a metric space
Let be a metric space
, and let . A function is called a càdlàg function if, for every ,
That is, ƒ is right-continuous with left limits.
mathematician
Anatoliy Skorokhod
. Skorokhod space can be assigned a topology
that, intuitively allows us to"wiggle space and time a bit" (whereas the traditional topology of uniform convergence only allows us to "wiggle space a bit"). For simplicity, take and — see Billingsley for a more general construction.
We must first define an analogue of the modulus of continuity
, . For any , set
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a càdlàg (French "continue à droite, limite à gauche"), RCLL (“right continuous with left limits”), or corlol (“continuous on (the) right, limit on (the) left”) function is a function defined on the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s (or a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of them) that is everywhere right-continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
and has left limit
Limit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
s everywhere. Càdlàg functions are important in the study of stochastic processes that admit (or even require) jumps, unlike Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
, which has continuous sample paths. The collection of càdlàg functions on a given domain is known as Skorokhod space.
Two related terms are càglàd, standing for "continue à gauche, limite à droite", the left-right reversal of càdlàg, and càllàl for"continue à l'un, limite à l’autre" (continuous on one side, limit on the other side), for a function which is interchangeably either càdlàg or càglàd at each point of the domain.
Definition

Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
, and let . A function is called a càdlàg function if, for every ,
- the left limit exists; and
- the right limit exists and equals ƒ(t).
That is, ƒ is right-continuous with left limits.
Examples
- All continuous functions are càdlàg functions.
- As a consequence of their definition, all cumulative distribution functionCumulative distribution functionIn probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
s are càdlàg functions. - The right derivative f+ of any convex functionConvex functionIn mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
f defined on an open interval, is an increasing cadlag function.
Skorokhod space
The set of all càdlàg functions from E to M is often denoted by (or simply D) and is called Skorokhod space after the UkrainianUkraine
Ukraine is a country in Eastern Europe. It has an area of 603,628 km², making it the second largest contiguous country on the European continent, after Russia...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Anatoliy Skorokhod
Anatoliy Skorokhod
Anatoliy Volodymyrovych Skorokhod was a Soviet and Ukrainian mathematician, and an academician of the National Academy of Sciences of Ukraine from 1985 to his death in 2011....
. Skorokhod space can be assigned a topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
that, intuitively allows us to"wiggle space and time a bit" (whereas the traditional topology of uniform convergence only allows us to "wiggle space a bit"). For simplicity, take and — see Billingsley for a more general construction.
We must first define an analogue of the modulus of continuity
Modulus of continuity
In mathematical analysis, a modulus of continuity is a function\omega:[0,\infty]\to[0,\infty]used to measure quantitatively the uniform continuity of functions. So, a function f:I\to\R admits \omega as a modulus of continuity if and only if|f-f|\leq\omega,for all x and y in the domain of f...
, . For any , set
-

and, for , define the càdlàg modulus to be-

where the infimumInfimumIn mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
runs over all partitions }, , with . This definition makes sense for non-càdlàg ƒ (just as the usual modulus of continuity makes sense for discontinuous functions) and it can be shown that ƒ is càdlàg if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
as .
Now let Λ denote the set of all strictly increasing, continuous bijectionBijectionA bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
s from E to itself (these are "wiggles in time"). Let-

denote the uniform norm on functions on E. Define the Skorokhod metric σ on D by-

where is the identity function. In terms of the"wiggle" intuition, measures the size of the"wiggle in time", and measures the size of the"wiggle in space".
It can be shown that the Skorokhod metricMetric (mathematics)In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
is, indeed a metric. The topology Σ generated by σ is called the Skorokhod topology on D.
Generalization of the uniform topology
The space C of continuous functions on E is a subspaceSubspace topologyIn topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
of D. The Skorokhod topology relativized to C coincides with the uniform topology there.
Completeness
It can be shown that, although D is not a complete spaceComplete spaceIn mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
with respect to the Skorokhod metric σ, there is a topologically equivalent metric σ0 with respect to which D is complete.
Separability
With respect to either σ or σ0, D is a separable space. Thus, Skorokhod space is a Polish spacePolish spaceIn the mathematical discipline of general topology, a Polish space is a separable completely metrizable topological space; that is, a space homeomorphic to a complete metric space that has a countable dense subset. Polish spaces are so named because they were first extensively studied by Polish...
.
Tightness in Skorokhod space
By an application of the Arzelà–Ascoli theorem, one can show that a sequence (μn)n=1,2,… of probability measureProbability measureIn mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
s on Skorokhod space D is tightTightness of measuresIn mathematics, tightness is a concept in measure theory. The intuitive idea is that a given collection of measures does not "escape to infinity."-Definitions:...
if and only if both the following conditions are met:-

and-

Algebraic and topological structure
Under the Skorokhod topology and pointwise addition of functions, D is not a topological group.
-
-
-
-
-

