Modulus of continuity
Encyclopedia
In mathematical analysis
, a modulus of continuity is a function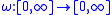
used to measure quantitatively the uniform continuity
of functions. So, a function
admits 
as a modulus of continuity if and only if
for all
and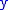 
in the domain of 
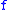. Since moduli of continuity are required to be infinitesimal at 0, a function turns out to be uniformly continuous if and only if it admits a modulus of continuity. Moreover, relevance to the notion is given by the fact that sets of functions sharing the same modulus of continuity are exactly equicontinuous families
. For instance, the modulus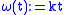
describes the k-Lipschitz functions, the moduli 
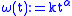describe the Hölder continuity, the modulus 
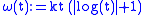describes the almost Lipschitz class, and so on. In general, the role of 
is to fix some explicit functional dependence of 
on 
in the 
definition of uniform continuity. The same notions generalize naturally to functions between metric spaces. Moreover, a suitable local version of these notions allows to describe quantitatively the continuity at a point in terms of moduli of continuity.
A special role is played by concave moduli of continuity, especially in connection with extension properties, and with approximation of uniformly continuous functions. For a function between metric spaces, it is equivalent to admit a modulus of continuity that is either concave, or subadditive, or uniformly continuous, or sublinear (in the sense of growth). Actually, the existence of such special moduli of continuity for a uniformly continuous function is always ensured whenever the domain is either a compact, or a convex subset of a normed space. However, a uniformly continuous function on a general metric space admits a concave modulus of continuity if and only if the ratios
are uniformly bounded for all pairs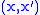 
bounded away from the diagonal of 
. The functions with the latter property constitute a special subclass of the uniformly continuous functions, that in the following we refer to as the special uniformly continuous functions.
Real-valued special uniformly continuous functions on the metric space
can also be characterized as the set of all functions that are restrictions to 
of uniformly continuous functions over any normed space isometrically containing 
. Also, it can be characterized as the uniform closure of the Lipschitz functions on 
.
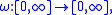
vanishing at 0 and continuous at 0, that is
Moduli of continuity are mainly used to give a quantitative account both of the continuity at a point, and of the uniform continuity, for functions between metric spaces, according to the following definitions.
A function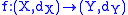
admits 
as (local) modulus of continuity at the point 
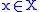if and only if,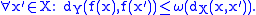
Also,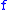
admits 
as (global) modulus of continuity if and only if,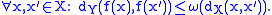
One equivalently says that
is a modulus of continuity (resp., at 
) for 
, or shortly,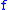 
is 
-continuous (resp., at 
). Here, we mainly treat the global notion.
Similarly, any function continuous at the point
admits a minimal modulus of continuity at 
(the (optimal) modulus of continuity of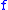 
at 
) :
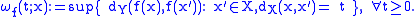
However, these restricted notions are not as relevant, for in most cases the optimal modulus of
could not be computed explicitly, but only bounded from above (by any modulus of continuity of f). Moreover, the main properties of moduli of continuity concern directly the unrestricted definition.
, or subadditive, or uniformly continuous, or sublinear. These properties are essentially equivalent in that, for a modulus
(more precisely, its restriction on 
) each of the following implies the next:
Thus, for a function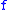
between metric spaces it is equivalent to admit a modulus of continuity which is either concave, or subadditive, or uniformly continuous, or sublinear. In this case, the function 
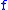is sometimes called a special uniformly continuous map.
This is always true in case of either compact or convex domains. Indeed, a uniformly continuous map
defined on a convex set
of a normed space 
always admits a subadditive modulus of continuity; in particular, real-valued as a function 
. Indeed, it is immediate to check that the optimal modulus of continuity 
defined above is subadditive if the domain of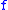 
is convex: we have, for all 
and 
:
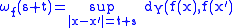
However, a uniformly continuous function on a general metric space admits a concave modulus of continuity if and only if the ratios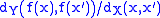
are uniformly bounded for all pairs 
bounded away from the diagonal of 
; this condition is certainly satisfied by any bounded uniformly continuous function; hence in particular, by any continuous function on a compact metric space.
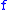is a uniformly continuous function with modulus of continuity 
, and 
is a 
Lipschitz function with uniform distance 
from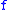 
, then 
admits the sublinear module of continuity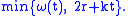 
Conversely, at least for real-valued functions, any bounded, uniformly continuous perturbation of a Lipschitz function is a special uniformly continuous function; indeed more is true as shown below. Note that as an immediate consequence, any uniformly continuous function on a convex subset of a normed space has a sublinear growth: there are constants 
and 
such that 
for all 
.
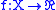defined on a subset 
of a normed space 
admits extensions over 
that preserves any subadditive modulus 
of 
. The least and the greatest of such extensions are respectively: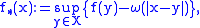
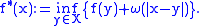
As remarked, any subadditive modulus of continuity is uniformly continuous: in fact, it admits itself as a modulus of continuity. Therefore,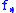
and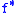 
are respectively inferior and superior envelopes of 
-continuous families; hence still 
-continuous.
Incidentally, by the Kuratowski embedding
any metric space is isometric to a subset of a normed space. Hence, special uniformly continuous real-valued functions are essentially the restrictions of uniformly continuous functions on normed spaces. In particular, this construction provides a quick proof of the Tietze extension theorem on compact metric spaces. However, for mappings with values in more general Banach spaces than
, the situation is quite more complicated; the first non-trivial result in this direction is the Kirszbraun theorem
.
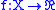defined on the metric space 
is uniformly approximable by means of Lipschitz functions. Moreover, the speed of convergence in terms of the Lipschitz constants of the approximations is strictly related to the modulus of continuity of 
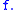Precisely, let 
be the minimal concave modulus of continuity of 
which is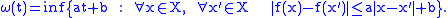
Let
be the uniform distance between the function 
and the set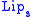 
of all Lipschitz real-valued functions on 
having Lipschitz constant 
:
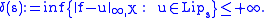
Then the functions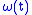
and 
can be related with each other via a Legendre transformation
: more precisely, the functions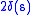
and 
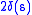(suitably extended to 
outside their domains of finiteness) are a pair of conjugated convex functions, for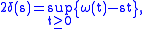
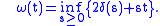
Since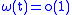
for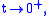 
it follows that 
for 
that exactly means that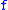 
is uniformly approximable by Lipschitz functions. Correspondingly, an optimal approximation is given by the functions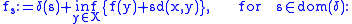
each function
has Lipschitz constant 
and 
in fact, it is the greatest 
Lipschitz function that realize the distance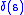 
. For example, the 
Hölder real-valued functions on a metric space are characterized as those functions that can be uniformly approximated by 
Lipschitz functions with speed of convergence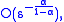 
while the almost Lipschitz functions are characterized by an exponential speed of convergence 
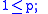let 
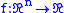a function of class 
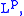and let 
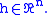The h-translation
of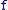
, that is the function
belongs to the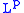
class; moreover, if 
, there holds
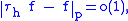as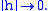 
Therefore, since translations are in fact
linear isometries, also
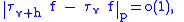as 
uniformly on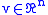
.
In other words, the map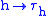
defines a strongly continuous group of linear isometries of 
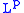. In the case 
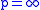the above property does not hold in general: actually, it exactly reduces to the uniform continuity, and defines the uniform continuous functions. This leads to the following definition, that generalizes the notion of a modulus of continuity of the uniformly continuous functions: a modulus of continuity 
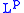for a measurable function 
is a modulus of continuity 
such that
This way, moduli of continuity also give a quantitative account of the continuity property shared by all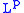
functions.
of first order:
If we replace that difference with a difference of order n we get a modulus of continuity of order n:
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, a modulus of continuity is a function
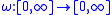
used to measure quantitatively the uniform continuity
Uniform continuity
In mathematics, a function f is uniformly continuous if, roughly speaking, it is possible to guarantee that f and f be as close to each other as we please by requiring only that x and y are sufficiently close to each other; unlike ordinary continuity, the maximum distance between x and y cannot...
of functions. So, a function
admits as a modulus of continuity if and only iffor all
and 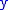in the domain of 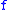. Since moduli of continuity are required to be infinitesimal at 0, a function turns out to be uniformly continuous if and only if it admits a modulus of continuity. Moreover, relevance to the notion is given by the fact that sets of functions sharing the same modulus of continuity are exactly equicontinuous familiesEquicontinuity
In mathematical analysis, a family of functions is equicontinuous if all the functions are continuous and they have equal variation over a given neighbourhood, in a precise sense described herein...
. For instance, the modulus
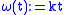describes the k-Lipschitz functions, the moduli 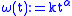describe the Hölder continuity, the modulus 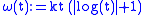describes the almost Lipschitz class, and so on. In general, the role of is to fix some explicit functional dependence of on 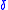in the 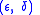definition of uniform continuity. The same notions generalize naturally to functions between metric spaces. Moreover, a suitable local version of these notions allows to describe quantitatively the continuity at a point in terms of moduli of continuity.A special role is played by concave moduli of continuity, especially in connection with extension properties, and with approximation of uniformly continuous functions. For a function between metric spaces, it is equivalent to admit a modulus of continuity that is either concave, or subadditive, or uniformly continuous, or sublinear (in the sense of growth). Actually, the existence of such special moduli of continuity for a uniformly continuous function is always ensured whenever the domain is either a compact, or a convex subset of a normed space. However, a uniformly continuous function on a general metric space admits a concave modulus of continuity if and only if the ratios
are uniformly bounded for all pairs 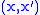bounded away from the diagonal of . The functions with the latter property constitute a special subclass of the uniformly continuous functions, that in the following we refer to as the special uniformly continuous functions.Real-valued special uniformly continuous functions on the metric space
can also be characterized as the set of all functions that are restrictions to of uniformly continuous functions over any normed space isometrically containing . Also, it can be characterized as the uniform closure of the Lipschitz functions on .Formal definition
Formally, a modulus of continuity is any real-extended valued function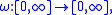vanishing at 0 and continuous at 0, that is
Moduli of continuity are mainly used to give a quantitative account both of the continuity at a point, and of the uniform continuity, for functions between metric spaces, according to the following definitions.
A function
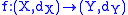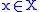admits as (local) modulus of continuity at the point if and only if,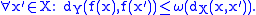Also,
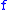admits as (global) modulus of continuity if and only if,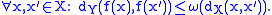One equivalently says that
is a modulus of continuity (resp., at ) for , or shortly, 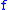is -continuous (resp., at ). Here, we mainly treat the global notion.Elementary facts
- If
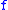has 
as modulus of continuity and 
, then, obviously, 
admits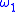 
too as modulus of continuity. - If
and 
are functions between metric spaces with moduli respectively 
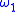and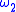 
, then the composition map 
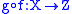has modulus of continuity 
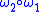. - If
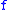and 
are functions from the metric space X to the Banach space 
, with moduli respectively 
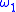and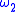 
, then any linear combination 
has modulus of continuity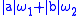 
. In particular, the set of all functions from 
to 
that have 
as a modulus of continuity is a convex subset of the vector space 
, closed under pointwise convergencePointwise convergenceIn mathematics, pointwise convergence is one of various senses in which a sequence of functions can converge to a particular function.-Definition:...
. - If
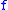and 
are bounded real-valued functions on the metric space 
, with moduli respectively 
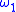and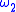 
, then the pointwise product 
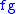has modulus of continuity 
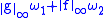. - If
is a family of real-valued functions on the metric space 
with common modulus of continuity 
, then the inferior envelope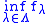 
, respectively, the superior envelope 
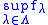, is a real-valued function with modulus of continuity 
, provided it is finite valued at every point. If 
is real-valued, it is sufficient that the envelope be finite at one point of 
at least.
Remarks
- Some authors require additional properties such as
being increasing, or continuous. However, if f admits a modulus of continuity in the weaker definition above, it also admits a modulus of continuity which is increasing and infinitely differentiable in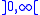 
. For instance,
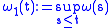is increasing, and 
;
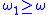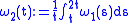is also continuous, and 
,
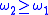- and a suitable variant of the preceding definition also makes
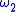infinitely differentiable in 
.
- Any uniformly continuous function admits a minimal modulus of continuity
, that is sometimes referred to as the (optimal) modulus of continuity of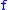 
:
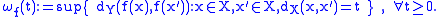
- Any uniformly continuous function admits a minimal modulus of continuity
Similarly, any function continuous at the point
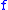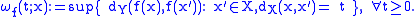
admits a minimal modulus of continuity at (the (optimal) modulus of continuity of at ) :However, these restricted notions are not as relevant, for in most cases the optimal modulus of
could not be computed explicitly, but only bounded from above (by any modulus of continuity of f). Moreover, the main properties of moduli of continuity concern directly the unrestricted definition.
- In general, the modulus of continuity of a uniformly continuous function on a metric space needs to take the value
For instance, the function 
such that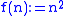 
is uniformly continuous with respect to the discrete metric on , and its minimal modulus of continuity is 
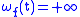for any positive integer 
, and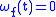 
otherwise. However, the situation is different for uniformly continuous functions defined on compact or convex subsets of normed spaces.
Special moduli of continuity
Special moduli of continuity also reflect certain global properties of functions such as extendibility and uniform approximation. In this section we mainly deal with moduli of continuity that are concaveConcave
The word concave means curving in or hollowed inward, as opposed to convex. The former may be used in reference to:* Concave lens, a lens with inward-curving surfaces.* Concave polygon, a polygon which is not convex....
, or subadditive, or uniformly continuous, or sublinear. These properties are essentially equivalent in that, for a modulus
(more precisely, its restriction on ) each of the following implies the next:
is concave;
is subadditive;
is uniformly continuous;
is sublinear, that is, there are constants 
and 
such that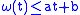 
for all 
;
is dominated by a concave modulus, that is, there exists a concave modulus of continuity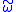 
such that 
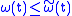for all 
.
Thus, for a function
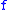between metric spaces it is equivalent to admit a modulus of continuity which is either concave, or subadditive, or uniformly continuous, or sublinear. In this case, the function 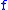is sometimes called a special uniformly continuous map.This is always true in case of either compact or convex domains. Indeed, a uniformly continuous map
defined on a convex setConvex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
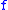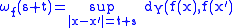
of a normed space always admits a subadditive modulus of continuity; in particular, real-valued as a function . Indeed, it is immediate to check that the optimal modulus of continuity defined above is subadditive if the domain of is convex: we have, for all and :However, a uniformly continuous function on a general metric space admits a concave modulus of continuity if and only if the ratios
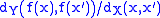are uniformly bounded for all pairs bounded away from the diagonal of ; this condition is certainly satisfied by any bounded uniformly continuous function; hence in particular, by any continuous function on a compact metric space.Sublinear moduli, and bounded perturbations from Lipschitz
A sublinear modulus of continuity can easily found for any uniformly function which is a bounded perturbations of a Lipschitz function: if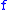 is a uniformly continuous function with modulus of continuity , and is a Lipschitz function with uniform distance from 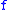, then admits the sublinear module of continuity 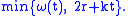Conversely, at least for real-valued functions, any bounded, uniformly continuous perturbation of a Lipschitz function is a special uniformly continuous function; indeed more is true as shown below. Note that as an immediate consequence, any uniformly continuous function on a convex subset of a normed space has a sublinear growth: there are constants and such that for all .Subadditive moduli, and extendibility
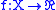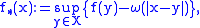
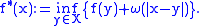
The above property for uniformly continuous function on convex domains admits a sort of converse at least in the case of real-valued functions: that is, every special uniformly continuous real-valued function defined on a subset of a normed space admits extensions over that preserves any subadditive modulus of . The least and the greatest of such extensions are respectively:As remarked, any subadditive modulus of continuity is uniformly continuous: in fact, it admits itself as a modulus of continuity. Therefore,
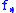and 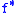are respectively inferior and superior envelopes of -continuous families; hence still -continuous.Incidentally, by the Kuratowski embedding
Kuratowski embedding
In mathematics, the Kuratowski embedding allows one to view any metric space as a subset of some Banach space. It is named after Kazimierz Kuratowski....
any metric space is isometric to a subset of a normed space. Hence, special uniformly continuous real-valued functions are essentially the restrictions of uniformly continuous functions on normed spaces. In particular, this construction provides a quick proof of the Tietze extension theorem on compact metric spaces. However, for mappings with values in more general Banach spaces than
, the situation is quite more complicated; the first non-trivial result in this direction is the Kirszbraun theoremKirszbraun theorem
In mathematics, specifically real analysis and functional analysis, the Kirszbraun theorem states that if U is a subset of some Hilbert space H1, and H2 is another Hilbert space, and...
.
Concave moduli, and Lipschitz approximation
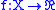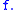Every special uniformly continuous real-valued function defined on the metric space is uniformly approximable by means of Lipschitz functions. Moreover, the speed of convergence in terms of the Lipschitz constants of the approximations is strictly related to the modulus of continuity of Precisely, let be the minimal concave modulus of continuity of which is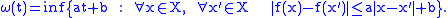Let
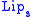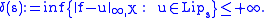
be the uniform distance between the function and the set of all Lipschitz real-valued functions on having Lipschitz constant :Then the functions
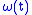and can be related with each other via a Legendre transformationLegendre transformation
In mathematics, the Legendre transformation or Legendre transform, named after Adrien-Marie Legendre, is an operation that transforms one real-valued function of a real variable into another...
: more precisely, the functions
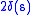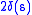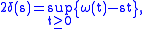
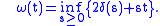
and (suitably extended to outside their domains of finiteness) are a pair of conjugated convex functions, forSince
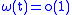for 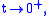it follows that for that exactly means that 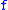is uniformly approximable by Lipschitz functions. Correspondingly, an optimal approximation is given by the functions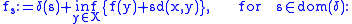each function
has Lipschitz constant and in fact, it is the greatest Lipschitz function that realize the distance 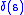. For example, the Hölder real-valued functions on a metric space are characterized as those functions that can be uniformly approximated by Lipschitz functions with speed of convergence 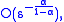while the almost Lipschitz functions are characterized by an exponential speed of convergence Examples of use
- Let
a continuous function. In the proof that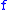 
is Riemann integrable, one usually bounds the distance between the upper and lower Riemann sums with respect to the Riemann partition 
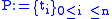in terms of the modulus of continuity of f and the modulus of the partition 
:
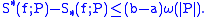
- For an example of use in the Fourier series, see Dini testDini testIn mathematics, the Dini and Dini-Lipschitz tests are highly precise tests that can be used to prove that the Fourier series of a function converges at a given point. These tests are named after Ulisse Dini and Rudolf Lipschitz.- Definition :...
.
History
Steffens (2006, p. 160) attributes the first usage of omega for the modulus of continuity to Lebesgue (1909, p. 309/p. 75) where omega refers to the oscillation of a Fourier transform. De la Vallée Poussin (1919, pp. 7-8) mentions both names (1) "modulus of continuity" and (2) "modulus of oscillation" and then concludes "but we choose (1) to draw attention to the usage we will make of it".The translation group of Lp functions, and moduli of continuity Lp.
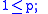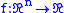Let let a function of class 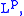and let 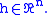The h-translationTranslation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
of
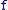, that is the functionbelongs to the
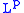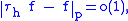class; moreover, if , there holds as 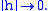Therefore, since translations are in fact
linear isometries, also
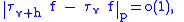as uniformly on
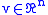.In other words, the map
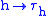defines a strongly continuous group of linear isometries of 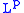. In the case 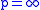the above property does not hold in general: actually, it exactly reduces to the uniform continuity, and defines the uniform continuous functions. This leads to the following definition, that generalizes the notion of a modulus of continuity of the uniformly continuous functions: a modulus of continuity 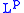for a measurable function is a modulus of continuity such thatThis way, moduli of continuity also give a quantitative account of the continuity property shared by all
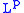functions.Modulus of continuity of higher orders
It can be seen that formal definition of the modulus uses notion of finite differenceFinite difference
A finite difference is a mathematical expression of the form f − f. If a finite difference is divided by b − a, one gets a difference quotient...
of first order:
If we replace that difference with a difference of order n we get a modulus of continuity of order n: