
Kuratowski embedding
Encyclopedia
In mathematics
, the Kuratowski embedding allows one to view any metric space
as a subset of some Banach space
. It is named after Kazimierz Kuratowski
.
Specifically, if (X,d) is a metric space, x0 is a point in X, and Cb(X) denotes the Banach space of all bounded continuous
real valued functions on X with the supremum norm, then the map
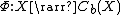
defined by
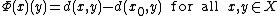
is an isometry
.
Note that this embedding depends on the chosen point x0 and is therefore not entirely canonical.
The Kuratowski–Wojdysławski theorem states that every bounded metric space X is isometric to a closed subset
of a convex
subset of some Banach space. (N.B. the image of this embedding is closed in the convex subset, not necessarily in the Banach space.) Here we use the isometry
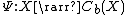
defined by

The convex set mentioned above is the convex hull
of Ψ(X).
In both of these embedding theorems, we may replace Cb(X) by the Banach space ℓ ∞(X) of all bounded functions X → R, again with the supremum norm, since Cb(X) is a closed linear subspace of ℓ ∞(X).
These embedding results are useful because Banach spaces have a number of useful properties not shared by all metric spaces: they are vector space
s which allows one to add points and do elementary geometry involving lines and planes etc.; and they are complete
. Given a function with codomain
X, it is frequently desirable to extend this function to a larger domain, and this often requires simultaneously enlarging the codomain to a Banach space containing X.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Kuratowski embedding allows one to view any metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
as a subset of some Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
. It is named after Kazimierz Kuratowski
Kazimierz Kuratowski
Kazimierz Kuratowski was a Polish mathematician and logician. He was one of the leading representatives of the Warsaw School of Mathematics.-Biography and studies:...
.
Specifically, if (X,d) is a metric space, x0 is a point in X, and Cb(X) denotes the Banach space of all bounded continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
real valued functions on X with the supremum norm, then the map
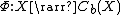
defined by
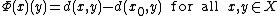
is an isometry
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
.
Note that this embedding depends on the chosen point x0 and is therefore not entirely canonical.
The Kuratowski–Wojdysławski theorem states that every bounded metric space X is isometric to a closed subset
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
of a convex
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
subset of some Banach space. (N.B. the image of this embedding is closed in the convex subset, not necessarily in the Banach space.) Here we use the isometry
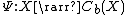
defined by

The convex set mentioned above is the convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of Ψ(X).
In both of these embedding theorems, we may replace Cb(X) by the Banach space ℓ ∞(X) of all bounded functions X → R, again with the supremum norm, since Cb(X) is a closed linear subspace of ℓ ∞(X).
These embedding results are useful because Banach spaces have a number of useful properties not shared by all metric spaces: they are vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s which allows one to add points and do elementary geometry involving lines and planes etc.; and they are complete
Complete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
. Given a function with codomain
Codomain
In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
X, it is frequently desirable to extend this function to a larger domain, and this often requires simultaneously enlarging the codomain to a Banach space containing X.
See also
- Tight spanTight spanIn metric geometry, the metric envelope or tight span of a metric space M is an injective metric space into which M can be embedded. In some sense it consists of all points "between" the points of M, analogous to the convex hull of a point set in a Euclidean space. The tight span is also sometimes...
, an embedding of any metric space into an injective metric spaceInjective metric spaceIn metric geometry, an injective metric space, or equivalently a hyperconvex metric space, is a metric space with certain properties generalizing those of the real line and of L∞ distances in higher-dimensional vector spaces...
defined similarly to the Kuratowski embedding

