In metric geometry, the metric envelope or tight span of a metric space

Metric space

In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...

 M is an injective metric space

Injective metric space

In metric geometry, an injective metric space, or equivalently a hyperconvex metric space, is a metric space with certain properties generalizing those of the real line and of L∞ distances in higher-dimensional vector spaces...

 into which M can be embedded. In some sense it consists of all points "between" the points of M, analogous to the convex hull

Convex hull

In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....

 of a point set in a Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

. The tight span is also sometimes known as the injective envelope or hyperconvex hull of M. It has also been called the injective hull, but should not be confused with the injective hull

Injective hull

In mathematics, especially in the area of abstract algebra known as module theory, the injective hull of a module is both the smallest injective module containing it and the largest essential extension of it...

 of a module

Module (mathematics)

In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...

 in algebra

Algebra

Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...

, a concept with a similar description relative to the category

Category (mathematics)

In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...

 of R-modules rather than metric spaces.

The tight span was first described by , and it was studied and applied by Holsztyński in the 1960s. It was later independently rediscovered by and ; see for this history. The tight span is one of the central constructions of T-theory

T-theory

T-theory is a branch of discrete mathematics dealing with analysis of trees and discrete metric spaces.-General history:As per Andreas Dress, T-theory originated from a question raised by Manfred Eigen, a recipient of the Nobel Prize in Chemistry, in the late seventies. He was trying to fit twenty...

.

Definition

The tight span of a finite metric space can be defined as follows. Let (X,d) be a metric space, with X finite, and let T(X) be the set of functions f from X to R such that

1. For any x, y in X, f(x) + f(y) ≥ d(x,y), and
2. For each x in X, there exists y in X such that f(x) + f(y) = d(x,y).

In particular (taking x = y in property 1 above) f(x) ≥ 0 for all x. One way to interpret the first requirement above is that f defines a set of possible distances from some new point to the points in X that must satisfy the triangle inequality

Triangle inequality

In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....

 together with the distances in (X,d). The second requirement states that none of these distances can be reduced without violating the triangle inequality.

Given two functions f and g in T(X), define δ(f,g) = max |f(x)-g(x)|; if we view T(X) as a subset of a vector space R^|X| then this is the usual L_∞ distance

Lp space

In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...

 between vectors. The tight span of X is the metric space (T(X),δ). There is an isometric embedding

Isometry

In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...

 of X into its tight span, given by mapping any x into the function f_x(y) = d(x,y). It is straightforward to expand the definition of δ using the triangle inequality for X to show that the distance between any two points of X is equal to the distance between the corresponding points in the tight span.

The definition above embeds the tight span of a set of n points into a space of dimension n. However, showed that, with a suitable general position assumption on the metric, this definition leads to a space with dimension between n/3 and n/2. provide an alternative definition of the tight span of a finite metric space, as the tropical convex hull

Tropical geometry

Tropical geometry is a relatively new area in mathematics, which might loosely be described as a piece-wise linear or skeletonized version of algebraic geometry. Its leading ideas had appeared in different guises in previous works of George M...

 of the vectors of distances from each point to each other point in the space.

For general (finite and infinite) metric spaces, the tight span may be defined using a modified version of property 2 in the definition above stating that inf f(x) + f(y) - d(x,y) = 0. An alternative definition based on the notion of a metric space aimed at its subspace

Metric space aimed at its subspace

In mathematics, a metric space aimed at its subspace is a categorical construction that has a direct geometric meaning. It is also a useful step toward the construction of the metric envelope, or tight span, which are basic objects of the category of metric spaces.Following , a notion of a metric...

 was described by , who proved that the injective envelope of a Banach space, in the category of Banach spaces, coincides (after forgetting the linear structure) with the tight span. This theorem allows to reduce certain problems from arbitrary Banach spaces to Banach spaces of the form  C(X), where X is a compact space.

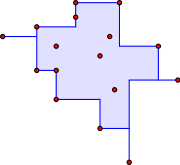
Example

The figure shows a set X of 16 points in the plane; to form a finite metric space from these points, we use the Manhattan distance (L₁ metric). The blue region shown in the figure is the orthogonal convex hull

Orthogonal convex hull

In Euclidean geometry, a set K\subset\R^n is defined to be orthogonally convex if, for every line L that is parallel to one of the axes of the Cartesian coordinate system, the intersection of K with L is empty, a point, or a single interval...

, the set of points z such that each of the four closed quadrants with z as apex contains a point of X. Any such point z corresponds to a point of the tight span: the function f(x) corresponding to a point z is f(x) = d(z,x). A function of this form satisfies property 1 of the tight span for any z in the Manhattan-metric plane, by the triangle inequality for the Manhattan metric. To show property 2 of the tight span, consider some point x in X; we must find y in X such that f(x)+f(y)=d(x,y). But if x is in one of the four quadrants having z as apex, y can be taken as any point in the opposite quadrant, so property 2 is satisfied as well. Conversely it can be shown that every point of the tight span corresponds in this way to a point in the orthogonal convex hull of these points. However, for point sets with the Manhattan metric in higher dimensions, and for planar point sets with disconnected orthogonal hulls, the tight span differs from the orthogonal convex hull.

Applications

describe applications of the tight span in reconstructing evolutionary trees

Phylogenetics

In biology, phylogenetics is the study of evolutionary relatedness among groups of organisms , which is discovered through molecular sequencing data and morphological data matrices...

 from biological data.

• The tight span serves a role in several online algorithm
  Online algorithm
  In computer science, an online algorithm is one that can process its input piece-by-piece in a serial fashion, i.e., in the order that the input is fed to the algorithm, without having the entire input available from the start. In contrast, an offline algorithm is given the whole problem data from...
  
  s for the K-server problem
  K-server problem
  The k-server problem is a problem of theoretical computer science in the category of online algorithms, one of two abstract problems on metric spaces that are central to the theory of competitive analysis...
  
  . uses the tight span to classify metric spaces on up to six points. uses the tight span to prove results about packing cut metrics into more general finite metric spaces.

See also

• Kuratowski embedding
  Kuratowski embedding
  In mathematics, the Kuratowski embedding allows one to view any metric space as a subset of some Banach space. It is named after Kazimierz Kuratowski....
  
  , an embedding of any metric space into a Banach space
  Banach space
  In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
  
  defined similarly to the tight span