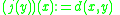Metric space aimed at its subspace
Encyclopedia
In mathematics
, a metric space aimed at its subspace is a categorical
construction that has a direct geometric meaning. It is also a useful step toward the construction of the metric envelope, or tight span
, which are basic (injective) objects of the category of metric space
s.
Following , a notion of a metric space Y aimed at its subspace X is defined.
Informally, imagine terrain Y, and its part X, such that wherever in Y you place a sharpshooter, and an apple at another place in Y, and then let the sharpshooter fire, the bullet will go through the apple and will always hit a point of X, or at least it will fly arbitrarily close to points of X – then we say that Y is aimed at X.
A priori, it may seem plausible that for a given X the superspaces Y that aim at X can be arbitrarily large or at least huge. We will see that this is not the case. Among the spaces, which aim at a subspace isometric to X there is a unique (up to
isometry
) universal one, Aim(X), which in a sense of canonical isometric embeddings contains any other space aimed at (an isometric image of) X. And in the special case of an arbitrary compact metric space X every bounded subspace of an arbitrary metric space Y aimed at X is totally bounded (i.e. its metric completion is compact).
be a metric space. Let 
be a subset of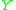 
, so that 
(the set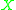 
with the metric from 
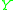restricted to 
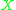) is a metric subspace of 
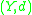. Then
Definition. Space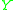
aims at 
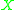if and only if, for all points 
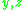of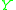 
, and for every real 
, there exists a point 
of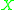 
such that
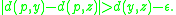
Let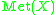
be the space of all real valued metric maps (non-contractive) of 
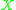. Define
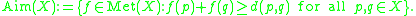
Then
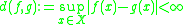
for every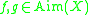
is a metric on 
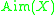. Furthermore, 
, where 
, is an isometric embedding of 
into 
; this is essentially a generalisation of the Kuratowski-Wojdysławski embedding of bounded metric spaces 
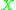into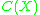 
, where we here consider arbitrary metric spaces (bounded or unbounded). It is clear that the space 
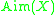is aimed at 
.
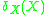be an isometric embedding. Then there exists a natural metric map 
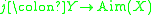such that 
:
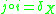for every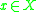
and 
.
Thus it follows that every space aimed at X can be isometrically mapped into Aim(X), with some additional (essential) categorical requirements satisfied.
The space Aim(X) is injective
(hyperconvex in the sense of Aronszajn-Panitchpakdi) – given a metric space M, which contains Aim(X) as a metric subspace, there is a canonical (and explicit) metric retraction of M onto Aim(X) .
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a metric space aimed at its subspace is a categorical
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
construction that has a direct geometric meaning. It is also a useful step toward the construction of the metric envelope, or tight span
Tight span
In metric geometry, the metric envelope or tight span of a metric space M is an injective metric space into which M can be embedded. In some sense it consists of all points "between" the points of M, analogous to the convex hull of a point set in a Euclidean space. The tight span is also sometimes...
, which are basic (injective) objects of the category of metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s.
Following , a notion of a metric space Y aimed at its subspace X is defined.
Informally, imagine terrain Y, and its part X, such that wherever in Y you place a sharpshooter, and an apple at another place in Y, and then let the sharpshooter fire, the bullet will go through the apple and will always hit a point of X, or at least it will fly arbitrarily close to points of X – then we say that Y is aimed at X.
A priori, it may seem plausible that for a given X the superspaces Y that aim at X can be arbitrarily large or at least huge. We will see that this is not the case. Among the spaces, which aim at a subspace isometric to X there is a unique (up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
isometry
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
) universal one, Aim(X), which in a sense of canonical isometric embeddings contains any other space aimed at (an isometric image of) X. And in the special case of an arbitrary compact metric space X every bounded subspace of an arbitrary metric space Y aimed at X is totally bounded (i.e. its metric completion is compact).
Definitions
Let be a metric space. Let be a subset of 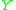, so that (the set 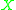with the metric from 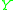restricted to 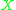) is a metric subspace of 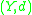. ThenDefinition. Space
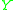aims at 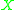if and only if, for all points 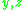of 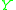, and for every real , there exists a point of 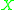such that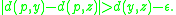Let
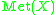be the space of all real valued metric maps (non-contractive) of 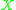. Define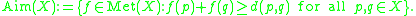Then
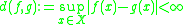
for every
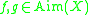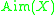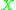is a metric on . Furthermore, , where , is an isometric embedding of into ; this is essentially a generalisation of the Kuratowski-Wojdysławski embedding of bounded metric spaces into 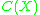, where we here consider arbitrary metric spaces (bounded or unbounded). It is clear that the space 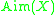is aimed at 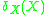.Properties
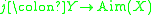Let be an isometric embedding. Then there exists a natural metric map such that :
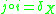for every
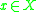and .- Theorem The space Y above is aimed at subspace X if and only if the natural mapping
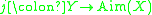is an isometric embedding.
Thus it follows that every space aimed at X can be isometrically mapped into Aim(X), with some additional (essential) categorical requirements satisfied.
The space Aim(X) is injective
Injective metric space
In metric geometry, an injective metric space, or equivalently a hyperconvex metric space, is a metric space with certain properties generalizing those of the real line and of L∞ distances in higher-dimensional vector spaces...
(hyperconvex in the sense of Aronszajn-Panitchpakdi) – given a metric space M, which contains Aim(X) as a metric subspace, there is a canonical (and explicit) metric retraction of M onto Aim(X) .