In Euclidean geometry

Euclidean geometry

Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...

, a set 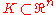is defined to be orthogonally convex if, for every line L that is parallel to one of the axes of the Cartesian coordinate system

Cartesian coordinate system

A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...

, the intersection of K with L is empty, a point, or a single interval. Unlike ordinary convex set

Convex set

In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...

s, an orthogonally convex set is not necessarily connected

Connectedness

In mathematics, connectedness is used to refer to various properties meaning, in some sense, "all one piece". When a mathematical object has such a property, we say it is connected; otherwise it is disconnected...

.

The orthogonal convex hull of a set 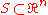is the intersection of all connected orthogonally convex supersets of S.

These definitions are made by analogy with the classical theory of convexity, in which K is convex

Convex set

In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...

 if, for every line L, the intersection of K with L is empty, a point, or a single interval. Orthogonal convexity restricts the lines for which this property is required to hold, so every convex set is orthogonally convex but not vice versa. For the same reason, the orthogonal convex hull itself is a subset of the convex hull

Convex hull

In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....

 of the same point set. A point p belongs to the orthogonal convex hull of S if and only if each of the closed axis-aligned orthant

Orthant

In geometry, an orthant or hyperoctant is the analogue in n-dimensional Euclidean space of a quadrant in the plane or an octant in three dimensions....

s having p as apex has a nonempty intersection with S.

The orthogonal convex hull is also known as the rectilinear convex hull, or the x-y convex hull.

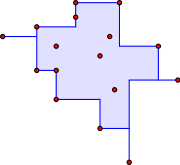
Example

The figure shows a set of 16 points in the plane and the orthogonal convex hull of these points. As can be seen in the figure, the orthogonal convex hull is a polygon

Polygon

In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...

 with some degenerate edges connecting extreme vertices in each coordinate direction. For a discrete point set such as this one, all orthogonal convex hull edges are horizontal or vertical. In this example, the orthogonal convex hull is connected.

Algorithms

Several authors have studied algorithms for constructing orthogonal convex hulls: ; ; ; . By the results of these authors, the orthogonal convex hull of n points in the plane may be constructed in time O(n log n), or possibly faster using integer searching data structures for points with integer coordinates.

Related concepts

It is natural to generalize orthogonal convexity to restricted-orientation convexity, in which a set K is defined to be convex if all lines having one of a finite set of slopes must intersect K in connected subsets; see e.g. , , or .

In addition, the tight span

Tight span

In metric geometry, the metric envelope or tight span of a metric space M is an injective metric space into which M can be embedded. In some sense it consists of all points "between" the points of M, analogous to the convex hull of a point set in a Euclidean space. The tight span is also sometimes...

 of a finite metric space is closely related to the orthogonal convex hull. If a finite point set in the plane has a connected orthogonal convex hull, that hull is the tight span for the Manhattan distance on the point set. However, orthogonal hulls and tight spans differ for point sets with disconnected orthogonal hulls, or in higher dimensional Lp space

Lp space

In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...

s.

describes several other results about orthogonal convexity and orthogonal visibility

Visibility (geometry)

Visibility is a mathematical abstraction of the real-life notion of visibility.Given a set of obstacles in the Euclidean space, two points in the space are said to be visible to each other, if the line segment that joins them does not intersect any obstacles.Computation of visibility is among the...

.