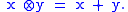Tropical geometry
Encyclopedia
Tropical geometry is a relatively new area in mathematics
, which might loosely be described as a piece-wise linear
or skeletonized version of algebraic geometry
. Its leading ideas had appeared in different guises in previous works of George M. Bergman and of Robert Bieri and John Groves, but only since the late nineties has an effort been made to consolidate the basic definitions of the theory. This effort has been in great part motivated by the strong applications to enumerative algebraic geometry
uncovered by Grigory Mikhalkin.
The adjective tropical is given in honor of the Brazil
ian mathematician Imre Simon
, who pioneered the field.
Consider the tropical semiring
(also known as the min-plus algebra
due to the definition of the semiring). This semiring, (R ∪ {∞}, ⊕, ⊗), is defined with the operations as follows:
A monomial in this semiring is a linear map, and a polynomial is the minimum of a finite number of such functions, and therefore a concave, piecewise linear function.
The set of points where a tropical polynomial F is non-differentiable is called its associated tropical hypersurface.
There are two important characterizations of these objects:
These two characterizations provide a "dictionary" between combinatorics and algebra. Such a dictionary can be used to take an algebraic problem and solve its easier combinatorial counterpart instead.
The tropical hypersurface can be generalized to a tropical variety by taking the non-archimedean amoeba of ideals I in K[x1, ..., xn] instead of polynomials. It has been proved that the tropical variety of an ideal I equals the intersection of the tropical hypersurfaces associated to every polynomial in I. This intersection can be chosen to be finite.
There are a number of articles and surveys on tropical geometry. The study of tropical curves (tropical hypersurfaces in R2) is particularly well developed. In fact, for this setting, mathematicians have established analogues of many classical theorems; e.g., Pappus's theorem
, Bézout's theorem
, the degree-genus formula, and the group law of the cubics
all have tropical counterparts.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, which might loosely be described as a piece-wise linear
Piecewise linear manifold
In mathematics, a piecewise linear manifold is a topological manifold together with a piecewise linear structure on it. Such a structure can be defined by means of an atlas, such that one can pass from chart to chart in it by piecewise linear functions.An isomorphism of PL manifolds is called a PL...
or skeletonized version of algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
. Its leading ideas had appeared in different guises in previous works of George M. Bergman and of Robert Bieri and John Groves, but only since the late nineties has an effort been made to consolidate the basic definitions of the theory. This effort has been in great part motivated by the strong applications to enumerative algebraic geometry
Enumerative geometry
In mathematics, enumerative geometry is the branch of algebraic geometry concerned with counting numbers of solutions to geometric questions, mainly by means of intersection theory.-History:...
uncovered by Grigory Mikhalkin.
The adjective tropical is given in honor of the Brazil
Brazil
Brazil , officially the Federative Republic of Brazil , is the largest country in South America. It is the world's fifth largest country, both by geographical area and by population with over 192 million people...
ian mathematician Imre Simon
Imre Simon
Imre Simon was a Hungarian-born Brazilian mathematician and computer scientist. His research mainly focused on theoretical computer science, Automata theory, and tropical mathematics, a subject he founded, and which was so named because he lived in Brazil. He was a professor of mathematics at the...
, who pioneered the field.
Basic definitions
We will use the min convention, that tropical addition is classical minimum. It is also possible to cast the whole subject in terms of the max convention, negating throughout, and several authors make this choice.Consider the tropical semiring
Semiring
In abstract algebra, a semiring is an algebraic structure similar to a ring, but without the requirement that each element must have an additive inverse...
(also known as the min-plus algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
due to the definition of the semiring). This semiring, (R ∪ {∞}, ⊕, ⊗), is defined with the operations as follows:
A monomial in this semiring is a linear map, and a polynomial is the minimum of a finite number of such functions, and therefore a concave, piecewise linear function.
The set of points where a tropical polynomial F is non-differentiable is called its associated tropical hypersurface.
There are two important characterizations of these objects:
- Tropical hypersurfaces are exactly the rational polyhedral complexes satisfying a "zero-tension" condition.
- Tropical surfaces are exactly the non-Archimedean amoebasAmoeba (mathematics)In complex analysis, a branch of mathematics, an amoeba is a set associated with a polynomial in one or more complex variables. Amoebas have applications in algebraic geometry...
over an algebraically closed field K with a non-Archimedean valuationValuation (mathematics)In algebra , a valuation is a function on a field that provides a measure of size or multiplicity of elements of the field...
.
These two characterizations provide a "dictionary" between combinatorics and algebra. Such a dictionary can be used to take an algebraic problem and solve its easier combinatorial counterpart instead.
The tropical hypersurface can be generalized to a tropical variety by taking the non-archimedean amoeba of ideals I in K[x1, ..., xn] instead of polynomials. It has been proved that the tropical variety of an ideal I equals the intersection of the tropical hypersurfaces associated to every polynomial in I. This intersection can be chosen to be finite.
There are a number of articles and surveys on tropical geometry. The study of tropical curves (tropical hypersurfaces in R2) is particularly well developed. In fact, for this setting, mathematicians have established analogues of many classical theorems; e.g., Pappus's theorem
Pappus's theorem
Pappus's theorem may refer to:*Pappus's centroid theorem*Pappus's hexagon theorem...
, Bézout's theorem
Bézout's theorem
Bézout's theorem is a statement in algebraic geometry concerning the number of common points, or intersection points, of two plane algebraic curves. The theorem claims that the number of common points of two such curves X and Y is equal to the product of their degrees...
, the degree-genus formula, and the group law of the cubics
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
all have tropical counterparts.
Introductory articles and surveys
- First Steps in Tropical Geometry
- Tropical geometry of statistical models
- The Tropical Grassmanian
- Enumerative tropical algebraic geometry in R2
- Amoebas of algebraic varieties and tropical geometry
- Tropical Mathematics
- Non-archimedean amoebas and tropical varieties
- Computing Tropical Varieties
- Tropical Geometry and its applications
- Tropical algebraic geometry