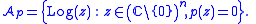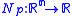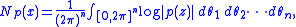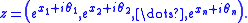In complex analysis

Complex analysis

Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...

, a branch of mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, an amoeba is a set associated with a polynomial

Polynomial

In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...

 in one or more complex variables

Several complex variables

The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...

. Amoebas have applications in algebraic geometry

Algebraic geometry

Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...

. There is independently a concept of "amoeba order" in set theory

Set theory

Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...

.

Definition

Consider the function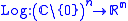


defined on the set of all n-tuple

Tuple

In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...

s 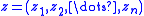of non-zero complex number

Complex number

A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

s with values in the Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

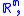  given by the formula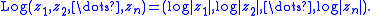

Here, 'log' denotes the natural logarithm

Natural logarithm

The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...

. If p(z) is a polynomial in complex variables, its amoeba is defined as the image

Image (mathematics)

In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...

 of the set of zeros of p under Log, so

Amoebas were introduced in 1994 in a book by Gelfand

Israel Gelfand

Israel Moiseevich Gelfand, also written Israïl Moyseyovich Gel'fand, or Izrail M. Gelfand was a Soviet mathematician who made major contributions to many branches of mathematics, including group theory, representation theory and functional analysis...

, Kapranov, and Zelevinsky

Andrei Zelevinsky

Andrei Zelevinsky is a mathematician who introduced the Bernstein–Zelevinsky classification of representations of p-adic groups, and cluster algebras....

.

Properties

• Any amoeba is a closed set
  Closed set
  In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
  
  .
• Any connected component
  Connected space
  In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
  
   of the complement
  Complement (set theory)
  In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
  
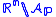    is convex
  Convex set
  In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
  
  .
• The area of an amoeba of a not identically zero polynomial in two complex variables is finite.
• A two-dimensional amoeba has a number of "tentacles" which are infinitely long and exponentially narrowing towards infinity.

Ronkin function

A useful tool in studying amoebas is the Ronkin function. For p(z) a polynomial in n complex variables, one defines the Ronkin function

by the formula

where denotes 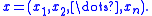Equivalently, is given by the integral

where

The Ronkin function is convex, and it is affine on each connected component of the complement of the amoeba of

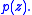
As an example, the Ronkin function of a monomial

Monomial

In mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...

with 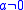is

Set theory

In set theory

Set theory

Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...

, the amoeba order is the set of pairs 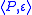where is an open subset of the Euclidean unit square with Lebesgue measure

Lebesgue measure

In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...

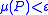. We order the elements of the amoeba order by .

External links

• Amoebas of algebraic varieties