JLO cocycle
Encyclopedia
In noncommutative geometry
, the JLO cocycle is a cocycle (and thus defines a cohomology class) in entire cyclic cohomology. It is a non-commutative version of the classic Chern character of the conventional differential geometry. In noncommutative geometry, the concept of a manifold is replaced by a noncommutative algebra
of "functions" on the putative noncommutative space. The cyclic cohomology of the algebra 
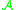contains the information about the topology of that noncommutative space, very much as the deRham cohomology contains the information about the topology of a conventional manifold.
The JLO cocycle is associated with a metric structure of non-commutative differential geometry known as a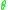
-summable Fredholm module (also known as a 
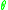-summable spectral triple
).
A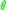 
-summable Fredholm module consists of the following data:
(a) A Hilbert space
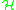such that 
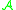acts on it as an algebra of bounded operators.
(b) A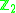
-grading 
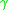on 
, 
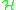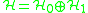. We assume that the algebra 
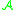is even under the 
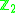-grading, i.e. 
, for all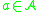 
.
(c) A self-adjoint (unbounded) operator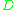
, called the Dirac operator such that
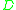is odd under 
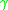, i.e. 
.
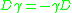Each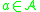
maps the domain of 
, 
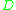into itself, and the operator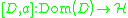 
is bounded.
, for all 
.
A classic example of a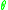
-summable Fredholm module arises as follows. Let 
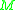be a compact spin manifold, 
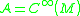, the algebra of smooth functions on 
, 
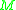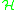the Hilbert space of square integrable forms on 
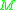, and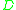 
the standard Dirac operator.
is a sequence
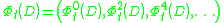
of functionals on the algebra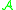
, where
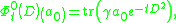
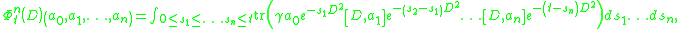
for
. The cohomology class defined by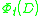 
is independent of the value of 
.
Noncommutative geometry
Noncommutative geometry is a branch of mathematics concerned with geometric approach to noncommutative algebras, and with construction of spaces which are locally presented by noncommutative algebras of functions...
, the JLO cocycle is a cocycle (and thus defines a cohomology class) in entire cyclic cohomology. It is a non-commutative version of the classic Chern character of the conventional differential geometry. In noncommutative geometry, the concept of a manifold is replaced by a noncommutative algebra
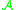of "functions" on the putative noncommutative space. The cyclic cohomology of the algebra contains the information about the topology of that noncommutative space, very much as the deRham cohomology contains the information about the topology of a conventional manifold.The JLO cocycle is associated with a metric structure of non-commutative differential geometry known as a
-summable Fredholm module (also known as a -summable spectral tripleSpectral triple
In noncommutative geometry and related branches of mathematics and mathematical physics, a spectral triple is a set of data which encodes geometric phenomenon in an analytic way. The definition typically involves a Hilbert space, an algebra of operators on it and an unbounded self-adjoint...
).
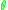-summable Fredholm Modules
A 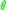-summable Fredholm module consists of the following data:(a) A Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
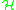such that 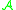acts on it as an algebra of bounded operators.(b) A
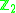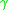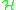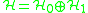-grading on , . We assume that the algebra 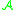is even under the 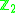-grading, i.e. , for all 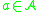.(c) A self-adjoint (unbounded) operator
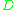, called the Dirac operator such that 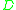is odd under 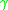, i.e. 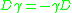.Each
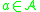maps the domain of 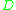, 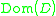into itself, and the operator 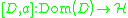is bounded., for all .A classic example of a
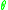-summable Fredholm module arises as follows. Let 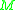be a compact spin manifold, 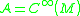, the algebra of smooth functions on 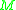, 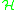the Hilbert space of square integrable forms on 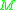, and 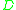the standard Dirac operator.The Cocycle
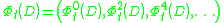
The JLO cocycle is a sequenceof functionals on the algebra
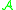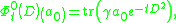
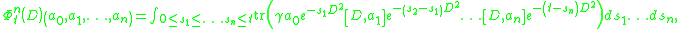
, wherefor
. The cohomology class defined by 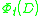is independent of the value of .External links
- http://projecteuclid.org/DPubS/Repository/1.0/Disseminate?view=body&id=pdf_1&handle=euclid.cmp/1104161905 - The original paper introducing the JLO cocycle.
- http://www.math.psu.edu/higson/Slides/trieste4.pdf - A nice set of lectures.
- [ftp://ftp.alainconnes.org/book94bigpdf.pdf] - A comprehensive account of noncommutative geometry by its creator.