Jacobi integral
Encyclopedia
In celestial mechanics
, Jacobi's integral (named after Carl Gustav Jacob Jacobi) is the only known conserved quantity for the restricted three-body problem problem [1]; unlike in the two-body problem, the energy and momentum of the system are not conserved separately and a general analytical solution is not possible. The integral has been used to derive numerous solutions in special cases.
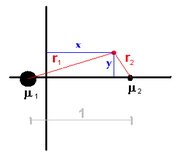One of the suitable coordinates system used is so called synodic or co-rotating system, placed at the barycentre, with the line connecting the two masses μ1, μ2 chosen as x-axis and the length unit equal to their distance. As the system co-rotates with the two masses, they remain stationary and positioned at (−μ2, 0) and (+μ1, 0)1.
In the (x, y)-coordinate system, the Jacobi constant is expressed as follows:
where:
Note that the Jacobi integral is minus twice the total energy per unit mass in the rotating frame of reference: the first term relates to centrifugal potential energy, the second represents gravitational potential and the third is the kinetic energy
.
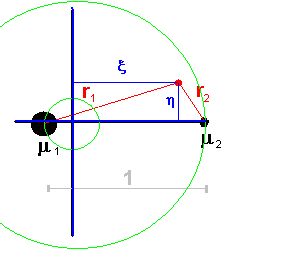In the inertial, sidereal co-ordinate system (ξ, η, ζ), the masses are orbiting the barycentre. In these co-ordinates the Jacobi constant is expressed by:
Using Lagrangian representation of the equations of motion:
[Eq.1]
[Eq.2]
[Eq.3]
Multiplying [Eq.1] , [Eq.2] and [Eq.3] by
and 
respectively and adding all three yields
Integrating yields
where CJ is the constant of integration.
The left side represents the square of the velocity v of the test particle in the co-rotating system.
1This co-ordinate system is non-inertial, which explains the appearance of terms related to centrifugal and Coriolis accelerations.
Celestial mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of celestial objects. The field applies principles of physics, historically classical mechanics, to astronomical objects such as stars and planets to produce ephemeris data. Orbital mechanics is a subfield which focuses on...
, Jacobi's integral (named after Carl Gustav Jacob Jacobi) is the only known conserved quantity for the restricted three-body problem problem [1]; unlike in the two-body problem, the energy and momentum of the system are not conserved separately and a general analytical solution is not possible. The integral has been used to derive numerous solutions in special cases.
Synodic system
In the (x, y)-coordinate system, the Jacobi constant is expressed as follows:
where:
is the mean motionMean motionMean motion, n\,\!, is a measure of how fast a satellite progresses around its elliptical orbit. Unless the orbit is circular, the mean motion is only an average value, and does not represent the instantaneous angular rate....
(orbital periodOrbital periodThe orbital period is the time taken for a given object to make one complete orbit about another object.When mentioned without further qualification in astronomy this refers to the sidereal period of an astronomical object, which is calculated with respect to the stars.There are several kinds of...
T)
, for the two masses m1, m2 and the gravitational constantGravitational constantThe gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
G
are distances of the test particle from the two masses
Note that the Jacobi integral is minus twice the total energy per unit mass in the rotating frame of reference: the first term relates to centrifugal potential energy, the second represents gravitational potential and the third is the kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
.
Sidereal system
Derivation
In the co-rotating system, the accelerations can be expressed as derivatives of a single scalar function
Using Lagrangian representation of the equations of motion:
[Eq.1]
[Eq.2]
[Eq.3]
Multiplying [Eq.1] , [Eq.2] and [Eq.3] by
and respectively and adding all three yields
Integrating yields
where CJ is the constant of integration.
The left side represents the square of the velocity v of the test particle in the co-rotating system.
1This co-ordinate system is non-inertial, which explains the appearance of terms related to centrifugal and Coriolis accelerations.