
Jacobi operator
Encyclopedia
A Jacobi operator, named after Carl Gustav Jakob Jacobi
, is a symmetric linear operator acting on sequence
s which is given by a tridiagonal matrix in the standard basis given by Kronecker deltas.
of square summable sequences over the positive integers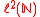 . In this case it is given by
. In this case it is given by
where the coefficients are assumed to satisfy
The operator will be bounded if and only if the coefficients are.
There are close connections with the theory of orthogonal polynomials
. In fact, the solution p(z,n) of the recurrence relation
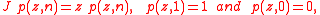
is a polynomial of degree n-1 and these polynomials are orthonormal with respect to the spectral measure corresponding to the first basis vector .
.
of the Toda lattice.
Carl Gustav Jakob Jacobi
Carl Gustav Jacob Jacobi was a German mathematician, widely considered to be the most inspiring teacher of his time and is considered one of the greatest mathematicians of his generation.-Biography:...
, is a symmetric linear operator acting on sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s which is given by a tridiagonal matrix in the standard basis given by Kronecker deltas.
Self-adjoint Jacobi operators
The most important case is the one of self-adjoint Jacobi operators acting on the Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
of square summable sequences over the positive integers
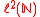 . In this case it is given by
. In this case it is given by
where the coefficients are assumed to satisfy

The operator will be bounded if and only if the coefficients are.
There are close connections with the theory of orthogonal polynomials
Orthogonal polynomials
In mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
. In fact, the solution p(z,n) of the recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
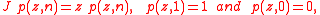
is a polynomial of degree n-1 and these polynomials are orthonormal with respect to the spectral measure corresponding to the first basis vector
 .
.Applications
It arises in many areas of mathematics and physics. The case a(n) = 1 is known as the discrete one-dimensional Schrödinger operator. It also arises in the Lax pairLax pair
In mathematics, in the theory of integrable systems, a Lax pair is a pair of time-dependent matrices or operators that describe the corresponding differential equations. They were introduced by Peter Lax to discuss solitons in continuous media...
of the Toda lattice.

