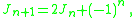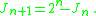Jacobsthal number
Encyclopedia
In mathematics
, the Jacobsthal numbers are an integer sequence
named after the German
mathematician
Ernst Jacobsthal
. Like the related Fibonacci number
s, they are a specific type of Lucas sequence
 for which P = 1, and Q = −2—and are defined by a similar recurrence relation
for which P = 1, and Q = −2—and are defined by a similar recurrence relation
: in simple terms, the sequence starts with 0 and 1, then each following number is found by adding the number before it to twice the number before that. The first Jacobsthal numbers are:
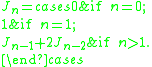
The next Jacobsthal number is also given by the recursion formula:
or by:
The first recursion formula above is also satisfied by the powers of2 .
The Jacobsthal number at a specific point in the sequence may be calculated directly using the closed-form equation:

The generating function for the Jacobsthal numbers is
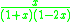 .
.
s, i.e. L0 = 2, and L1 = 1; they are defined by the recurrence relation:
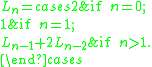
The following Jacobsthal-Lucas number also satisfies:
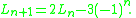
The Jacobsthal-Lucas number at a specific point in the sequence may be calculated directly using the closed-form equation:
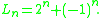
The first Jacobsthal-Lucas numbers are:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Jacobsthal numbers are an integer sequence
Integer sequence
In mathematics, an integer sequence is a sequence of integers.An integer sequence may be specified explicitly by giving a formula for its nth term, or implicitly by giving a relationship between its terms...
named after the German
Germany
Germany , officially the Federal Republic of Germany , is a federal parliamentary republic in Europe. The country consists of 16 states while the capital and largest city is Berlin. Germany covers an area of 357,021 km2 and has a largely temperate seasonal climate...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Ernst Jacobsthal
Ernst Jacobsthal
Ernst Erich Jacobsthal was a German mathematician, and brother to the archaeologist Paul Jacobsthal....
. Like the related Fibonacci number
Fibonacci number
In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
s, they are a specific type of Lucas sequence
Lucas sequence
In mathematics, the Lucas sequences Un and Vn are certain integer sequences that satisfy the recurrence relationwhere P and Q are fixed integers...
 for which P = 1, and Q = −2—and are defined by a similar recurrence relation
for which P = 1, and Q = −2—and are defined by a similar recurrence relationRecurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
: in simple terms, the sequence starts with 0 and 1, then each following number is found by adding the number before it to twice the number before that. The first Jacobsthal numbers are:
- 00 (number)0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
, 1, 1, 3, 5, 1111 (number)11 is the natural number following 10 and preceding 12.Eleven is the first number which cannot be counted with a human's eight fingers and two thumbs additively. In English, it is the smallest positive integer requiring three syllables and the largest prime number with a single-morpheme name...
, 2121 (number)21 is the natural number following 20 and preceding 22.-In mathematics:Twenty-one is the fifth discrete Semiprime and the second in the family. With 22 it forms the second discrete Semiprime pair...
, 4343 (number)43 is the natural number following 42 and preceding 44.- In mathematics :Forty-three is the 14th smallest prime number. The previous is forty-one, with which it comprises a twin prime, and the next is forty-seven. 43 is the smallest prime that is not a Chen prime...
, 8585 (number)85 is the natural number following 84 and preceding 86.-In mathematics:85 is an octahedral number, a centered triangular number, a centered square number, a decagonal number, and a Smith number....
, 171171 (number)171 is the natural number following 170 and preceding 172.-In mathematics:* 171 is an odd number* 171 is a composite number* 171 is a deficient number* 171 is a Harshad number, divisible by the sum of its digits...
, 341, 683, 1365, 2731, 5461, 10923, 21845, 43691, 87381, 174763, 349525, …
Jacobsthal numbers
Jacobsthal numbers are defined by the recurrence relation: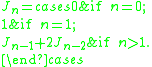
The next Jacobsthal number is also given by the recursion formula:
or by:
The first recursion formula above is also satisfied by the powers of
The Jacobsthal number at a specific point in the sequence may be calculated directly using the closed-form equation:

The generating function for the Jacobsthal numbers is
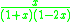 .
.Jacobsthal-Lucas numbers
Jacobsthal-Lucas numbers retain the recurrence relation, Ln-1 + 2Ln-2, of Jacobsthal numbers, but use the starting conditions of the Lucas numberLucas number
The Lucas numbers are an integer sequence named after the mathematician François Édouard Anatole Lucas , who studied both that sequence and the closely related Fibonacci numbers...
s, i.e. L0 = 2, and L1 = 1; they are defined by the recurrence relation:
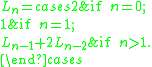
The following Jacobsthal-Lucas number also satisfies:
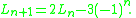
The Jacobsthal-Lucas number at a specific point in the sequence may be calculated directly using the closed-form equation:
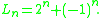
The first Jacobsthal-Lucas numbers are:
- 2, 1, 5, 7, 1717 (number)17 is the natural number following 16 and preceding 18. It is prime.In spoken English, the numbers 17 and 70 are sometimes confused because they sound similar. When carefully enunciated, they differ in which syllable is stressed: 17 vs 70...
, 3131 (number)31 is the natural number following 30 and preceding 32.- In mathematics :Thirty-one is the third Mersenne prime as well as the fourth primorial prime, and together with twenty-nine, another primorial prime, it comprises a twin prime. As a Mersenne prime, 31 is related to the perfect number 496,...
, 6565 (number)65 is the natural number following 64 and preceding 66.-In mathematics:Sixty-five is the 23rd semiprime and the 3rd of the form it is an octagonal number. It is also a Cullen number...
, 127127 (number)127 is the natural number following 126 and preceding 128.- In mathematics :*As a Mersenne prime, 127 is related to the perfect number 8128. 127 is also an exponent for the Mersenne prime 2127 - 1, making 127 a double Mersenne prime...
, 257, 511, 1025, 2047, 4097, 8191, 16385, 32767, 65537, 131071, 262145, 524287, 1048577, …