Jeans equations
Encyclopedia
The Jeans equations describe the motion of a collection of stars in a gravitational field.
If ν = ν(x,t) is the density of stars in space, as a function of position x = (x1, x2, x3) and time t, v = (v1, v2, v3) is the velocity, and Φ = Φ(x,t) is the gravitational potential,
the Jeans equations may be written as
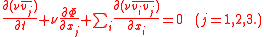
Here, the bar is used to take averages at a given point, so that, for example,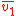
is the average of component 1 of the velocity of the stars at a given point.
The second set of equations may alternately be written as
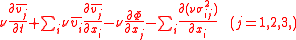
where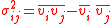
measures the velocity dispersion in components i and j at a given point.
The Jeans equations are analogous to the Euler equations for fluid flow and may be derived from the collisionless Boltzmann equation. They were originally derived by James Clerk Maxwell
but were first applied to stellar dynamics by James Jeans.
If ν = ν(x,t) is the density of stars in space, as a function of position x = (x1, x2, x3) and time t, v = (v1, v2, v3) is the velocity, and Φ = Φ(x,t) is the gravitational potential,
the Jeans equations may be written as
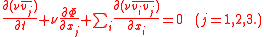
Here, the bar is used to take averages at a given point, so that, for example,
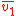is the average of component 1 of the velocity of the stars at a given point.The second set of equations may alternately be written as
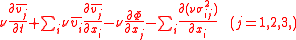
where
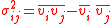measures the velocity dispersion in components i and j at a given point.The Jeans equations are analogous to the Euler equations for fluid flow and may be derived from the collisionless Boltzmann equation. They were originally derived by James Clerk Maxwell
James Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
but were first applied to stellar dynamics by James Jeans.