Jet group
Encyclopedia
In mathematics
, a jet group is a generalization of the general linear group
which applies to Taylor polynomials instead of vectors at a point. Essentially a jet group describes how a Taylor polynomial transforms under changes of coordinate system
s (or, equivalently, diffeomorphism
s).
The k-th order jet group Gnk consists of jet
s of smooth diffeomorphisms
such that φ(0)=0.
The following is a more precise definition of the jet group.
Let
. The gradient of a function 
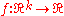can be interpreted as a section of the cotangent bundle of 
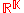given by 
. Similarly, derivatives of order up to 
are sections of the jet bundle 
, where
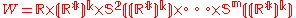
and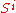
denotes the 
symmetric power. A function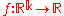 
has a prolongation 
defined at each point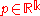 
by placing the 
partials of 
at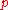 
in the 
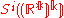component of 
.
Consider a point
. There is a unique polynomial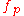 
in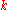 
variables and of order 
such that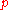 
is in the image of 
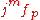. That is, 
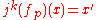. The differential data 
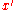may be transferred to lie over another point 
as 
, the partials of 
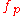over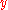 
.
Provide
with a group structure by taking
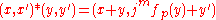
With this group structure,
is a Carnot group
of class
.
Because of the properties of jets under function composition
, Gnk is a Lie group
. The jet group is a semidirect product
of the general linear group and a connected, simply connected nilpotent Lie group. It is also in fact an algebraic group
, since the composition involves only polynomial operations.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a jet group is a generalization of the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
which applies to Taylor polynomials instead of vectors at a point. Essentially a jet group describes how a Taylor polynomial transforms under changes of coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
s (or, equivalently, diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
s).
The k-th order jet group Gnk consists of jet
Jet (mathematics)
In mathematics, the jet is an operation which takes a differentiable function f and produces a polynomial, the truncated Taylor polynomial of f, at each point of its domain...
s of smooth diffeomorphisms
- φ:Rn→Rn
such that φ(0)=0.
The following is a more precise definition of the jet group.
Let
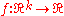. The gradient of a function can be interpreted as a section of the cotangent bundle of 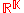given by . Similarly, derivatives of order up to are sections of the jet bundle , where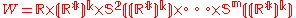and
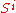denotes the symmetric power. A function 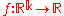has a prolongation defined at each point 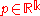by placing the partials of at 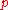in the 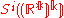component of .Consider a point
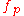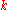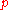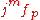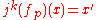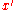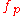. There is a unique polynomial in variables and of order such that is in the image of . That is, . The differential data may be transferred to lie over another point as , the partials of over 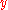.Provide
with a group structure by taking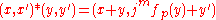With this group structure,
is a Carnot groupCarnot group
In mathematics, a Carnot group is a simply connected nilpotent Lie group, together with a derivation of its Lie algebra such that the subspace with eigenvalue 1 generates the Lie algebra. Carnot groups have a Carnot–Carathéodory metric. They were introduced by and ....
of class
.Because of the properties of jets under function composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
, Gnk is a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
. The jet group is a semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of the general linear group and a connected, simply connected nilpotent Lie group. It is also in fact an algebraic group
Algebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
, since the composition involves only polynomial operations.