
Juggler sequence
Encyclopedia
In recreational mathematics
a juggler sequence is an integer sequence
that starts with a positive integer a0, with each subsequent term in the sequence defined by the recurrence relation
:
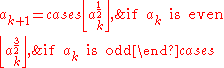
. The name is derived from the rising and falling nature of the sequences, like balls in the hands of a juggler.
For example, the juggler sequence starting with a0 = 3 is
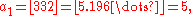
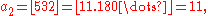
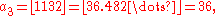


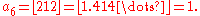
If a juggler sequence reaches 1, then all subsequent terms are equal to 1. It is conjectured that all juggler sequences eventually reach 1. This conjecture has been verifed for initial terms up to 106, but has not been proved. Juggler sequences therefore present a problem that is similar to the Collatz conjecture
, about which Paul Erdős
stated that "mathematics is not yet ready for such problems".
For a given initial term n we define l(n) to be the number of steps which the juggler sequence starting at n takes to first reach 1, and h(n) to be the maximum value in the juggler sequence starting at n. For small values of n we have:
Juggler sequences can reach very large values before descending to 1. For example, the juggler sequence starting at a0 = 37 reaches a maximum value of 24906114455136. Harry J. Smith has determined that the juggler sequence starting at a0 = 48443 reaches a maximum value at a60 with 972,463 digits, before reaching 1 at a157.
Recreational mathematics
Recreational mathematics is an umbrella term, referring to mathematical puzzles and mathematical games.Not all problems in this field require a knowledge of advanced mathematics, and thus, recreational mathematics often attracts the curiosity of non-mathematicians, and inspires their further study...
a juggler sequence is an integer sequence
Integer sequence
In mathematics, an integer sequence is a sequence of integers.An integer sequence may be specified explicitly by giving a formula for its nth term, or implicitly by giving a relationship between its terms...
that starts with a positive integer a0, with each subsequent term in the sequence defined by the recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
:
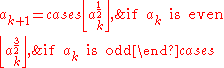
Background
Juggler sequences were publicised by American mathematician and author Clifford A. PickoverClifford A. Pickover
Clifford A. Pickover is an American author, editor, and columnist in the fields of science, mathematics, and science fiction, and is employed at the IBM Thomas J. Watson Research Center in Yorktown, New York.- Biography :He received his Ph.D...
. The name is derived from the rising and falling nature of the sequences, like balls in the hands of a juggler.
For example, the juggler sequence starting with a0 = 3 is
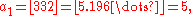
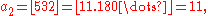
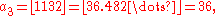


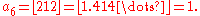
If a juggler sequence reaches 1, then all subsequent terms are equal to 1. It is conjectured that all juggler sequences eventually reach 1. This conjecture has been verifed for initial terms up to 106, but has not been proved. Juggler sequences therefore present a problem that is similar to the Collatz conjecture
Collatz conjecture
The Collatz conjecture is a conjecture in mathematics named after Lothar Collatz, who first proposed it in 1937. The conjecture is also known as the 3n + 1 conjecture, the Ulam conjecture , Kakutani's problem , the Thwaites conjecture , Hasse's algorithm The Collatz conjecture is a...
, about which Paul Erdős
Paul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
stated that "mathematics is not yet ready for such problems".
For a given initial term n we define l(n) to be the number of steps which the juggler sequence starting at n takes to first reach 1, and h(n) to be the maximum value in the juggler sequence starting at n. For small values of n we have:
| n | Juggler sequence | l(n) |
h(n) |
|---|---|---|---|
| 2 | 2, 1 | 1 | 2 |
| 3 | 3, 5, 11, 36, 6, 2, 1 | 6 | 36 |
| 4 | 4, 2, 1 | 2 | 4 |
| 5 | 5, 11, 36, 6, 2, 1 | 5 | 36 |
| 6 | 6, 2, 1 | 2 | 6 |
| 7 | 7, 18, 4, 2, 1 | 4 | 18 |
| 8 | 8, 2, 1 | 2 | 8 |
| 9 | 9, 27, 140, 11, 36, 6, 2, 1 | 7 | 140 |
| 10 | 10, 3, 5, 11, 36, 6, 2, 1 | 7 | 36 |
Juggler sequences can reach very large values before descending to 1. For example, the juggler sequence starting at a0 = 37 reaches a maximum value of 24906114455136. Harry J. Smith has determined that the juggler sequence starting at a0 = 48443 reaches a maximum value at a60 with 972,463 digits, before reaching 1 at a157.
External links
- Juggler sequence calculator at Collatz Conjecture Calculation Center
- Juggler Number pages by Harry J. Smith

