Jump search
Encyclopedia
In computer science
, a jump search or block search refers to a search algorithm
for ordered lists. It works by first checking all items Lkm, where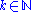
and m is the block size, until an item is found that is larger than the search key. To find the exact position of the search key in the list a linear search
is performed on the sublist L[(k-1)m, km].
The optimal value of m is √n, where n is the length of the list L. Because both steps of the algorithm
look at, at most, √n items the algorithm runs in O(√n) time. This is better than a linear search
, but worse than a binary search. The advantage over the latter is that a jump search only needs to jump backwards once, while a binary can jump backwards up to log n times. This can be important if a jumping backwards takes significantly more time than jumping forward.
The algorithm can be modified by performing multiple levels of jump search on the sublists, before finally performing the linear search
. For an k-level jump search the optimum block size ml for the lth level (counting from 1) is n(k-l)/k. The modified algorithm will perform k backward jumps and runs in O(kn1/(k+1)) time.
Algorithm JumpSeach
Input: An ordered list L, its length n and a search key s.
Output: The position of s in L, or nothing if s is not in L.
a ← 0
b ← ⌊√n⌋
while Lmin(b,n)-1 < s do
a ← b
b ← b + ⌊√n⌋
if a ≥ n then
return nothing
while La < s do
a ← a + 1
if a = min(b,n)
return nothing
if La = s then
return a
else
return nothing
C:
//Performs a jump search of the integer array "arr[]" of length "len" for search key "key".
int jumpsearch(int arr[], int len, int key) {
int a = 0;
int b = (int)floor(sqrt(len));
while (arr[(b < len ? b : len)-1] < key) {
a = b;
b = b + (int)floor(sqrt(len));
if (a >= len) {
return -1;
}
}
while (arr[a] < key) {
a++;
if (a (b < len ? b : len)) {
key) {
return a;
} else {
return -1;
}
}
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, a jump search or block search refers to a search algorithm
Search algorithm
In computer science, a search algorithm is an algorithm for finding an item with specified properties among a collection of items. The items may be stored individually as records in a database; or may be elements of a search space defined by a mathematical formula or procedure, such as the roots...
for ordered lists. It works by first checking all items Lkm, where
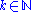and m is the block size, until an item is found that is larger than the search key. To find the exact position of the search key in the list a linear searchLinear search
In computer science, linear search or sequential search is a method for finding a particular value in a list, that consists of checking every one of its elements, one at a time and in sequence, until the desired one is found....
is performed on the sublist L[(k-1)m, km].
The optimal value of m is √n, where n is the length of the list L. Because both steps of the algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
look at, at most, √n items the algorithm runs in O(√n) time. This is better than a linear search
Linear search
In computer science, linear search or sequential search is a method for finding a particular value in a list, that consists of checking every one of its elements, one at a time and in sequence, until the desired one is found....
, but worse than a binary search. The advantage over the latter is that a jump search only needs to jump backwards once, while a binary can jump backwards up to log n times. This can be important if a jumping backwards takes significantly more time than jumping forward.
The algorithm can be modified by performing multiple levels of jump search on the sublists, before finally performing the linear search
Linear search
In computer science, linear search or sequential search is a method for finding a particular value in a list, that consists of checking every one of its elements, one at a time and in sequence, until the desired one is found....
. For an k-level jump search the optimum block size ml for the lth level (counting from 1) is n(k-l)/k. The modified algorithm will perform k backward jumps and runs in O(kn1/(k+1)) time.
Implementation
Psuedocode:Algorithm JumpSeach
Input: An ordered list L, its length n and a search key s.
Output: The position of s in L, or nothing if s is not in L.
a ← 0
b ← ⌊√n⌋
while Lmin(b,n)-1 < s do
a ← b
b ← b + ⌊√n⌋
if a ≥ n then
return nothing
while La < s do
a ← a + 1
if a = min(b,n)
return nothing
if La = s then
return a
else
return nothing
C:
//Performs a jump search of the integer array "arr[]" of length "len" for search key "key".
int jumpsearch(int arr[], int len, int key) {
int a = 0;
int b = (int)floor(sqrt(len));
while (arr[(b < len ? b : len)-1] < key) {
a = b;
b = b + (int)floor(sqrt(len));
if (a >= len) {
return -1;
}
}
while (arr[a] < key) {
a++;
if (a
(b < len ? b : len)) {
return -1;
}
}
if (arr[a]
key) {return a;
} else {
return -1;
}
}
See also
- Jump list
- Interpolation searchInterpolation searchInterpolation search is an algorithm for searching for a given key value in an indexed array that has been ordered by the values of the key. It parallels how humans search through a telephone book for a particular name, the key value by which the book's entries are ordered...
- Linear searchLinear searchIn computer science, linear search or sequential search is a method for finding a particular value in a list, that consists of checking every one of its elements, one at a time and in sequence, until the desired one is found....
- runs in O(n) time, only looks forward - Binary search - runs in O(log n) time, looks both forward and backward