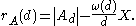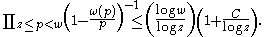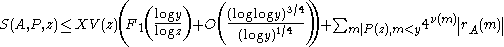Jurkat–Richert theorem
Encyclopedia
The Jurkat–Richert theorem is a mathematical theorem in sieve theory
. It is a key ingredient in proofs of Chen's theorem
on Goldbach's conjecture
.
It was proved in 1965 by Wolfgang B. Jurkat and Hans-Egon Richert
.
.
Other formulations are in Jurkat & Richert, Halberstam & Richert,
and Nathanson.
Suppose A is a finite sequence of integers and P is a set of primes. Write Ad for the number of items in A that are divisible by d, and write P(z) for the product of the elements in P that are less than z. Write ω(d) for a multiplicative function
such that ω(p)/p is approximately the proportion of elements of A divisible by p, write X for any convenient approximation to |A|, and write the remainder as
Write S(A,P,z) for the number of items in A that are relatively prime to P(z). Write
Write ν(m) for the number of distinct prime divisors of m. Write F1 and f1 for functions satisfying certain difference differential equations (see Diamond & Halberstam for the definition and properties).
We assume the dimension (sifting density) is 1: that is, there is a constant C such that for 2 ≤ z < w we have
(The book of Diamond & Halberstam extends the theorem to dimensions higher than 1.) Then the Jurkat–Richert theorem states that for any numbers y and z with 2 ≤ z ≤ y ≤ X we have
and
Sieve theory
Sieve theory is a set of general techniques in number theory, designed to count, or more realistically to estimate the size of, sifted sets of integers. The primordial example of a sifted set is the set of prime numbers up to some prescribed limit X. Correspondingly, the primordial example of a...
. It is a key ingredient in proofs of Chen's theorem
Chen's theorem
right|thumb|Chen JingrunChen's theorem states that every sufficiently large even number can be written as the sum of either two primes, or a prime and a semiprime . The theorem was first stated by Chinese mathematician Chen Jingrun in 1966, with further details of the proof in 1973. His original...
on Goldbach's conjecture
Goldbach's conjecture
Goldbach's conjecture is one of the oldest unsolved problems in number theory and in all of mathematics. It states:A Goldbach number is a number that can be expressed as the sum of two odd primes...
.
It was proved in 1965 by Wolfgang B. Jurkat and Hans-Egon Richert
Hans-Egon Richert
Hans-Egon Richert was a German mathematician who worked primarily in analytic number theory. He is the author of a definitive bookon sieve theory.-Life and education:...
.
Statement of the theorem
This formulation is from Diamond & HalberstamHeini Halberstam
Heini Halberstam is a British mathematician, working in the field of analytic number theory. He is one of the two mathematicians after whom the Elliott-Halberstam conjecture is named....
.
Other formulations are in Jurkat & Richert, Halberstam & Richert,
and Nathanson.
Suppose A is a finite sequence of integers and P is a set of primes. Write Ad for the number of items in A that are divisible by d, and write P(z) for the product of the elements in P that are less than z. Write ω(d) for a multiplicative function
Multiplicative function
In number theory, a multiplicative function is an arithmetic function f of the positive integer n with the property that f = 1 and whenevera and b are coprime, then...
such that ω(p)/p is approximately the proportion of elements of A divisible by p, write X for any convenient approximation to |A|, and write the remainder as
Write S(A,P,z) for the number of items in A that are relatively prime to P(z). Write
Write ν(m) for the number of distinct prime divisors of m. Write F1 and f1 for functions satisfying certain difference differential equations (see Diamond & Halberstam for the definition and properties).
We assume the dimension (sifting density) is 1: that is, there is a constant C such that for 2 ≤ z < w we have
(The book of Diamond & Halberstam extends the theorem to dimensions higher than 1.) Then the Jurkat–Richert theorem states that for any numbers y and z with 2 ≤ z ≤ y ≤ X we have
and