Jónsson function
Encyclopedia
In set theory
, a mathematical discipline, an ω-Jónsson function, named for Bjarni Jónsson
, for a set of ordinals x is a function from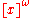
to x such that for any subset y of x with the same cardinality as x, f restricted to 
maps onto x. Here if x is an ordered set and α is an ordinal, 
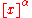is the set of subsets of x of order type α. So in particular 
is the set of strictly increasing sequences of x.
showed that for any ordinal λ there is an ω-Jónsson function for λ.
Kunen's proof of Kunen's inconsistency theorem
uses a Jónsson function for cardinals λ such that 2λ = λℵ0, and Kunen observed that for this special case there is a simpler proof of the existence of Jónsson functions. gave a simple proof for the general case.
The existence of Jónsson functions shows that for any cardinal there is an algebra with an infinitary operation that has no proper subalgebras of the same cardinality. In particular if infinitary operations are allowed then an analogue of Jónsson algebras exists in any cardinality, so there are no infinitary analogues of Jónsson cardinal
s.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, a mathematical discipline, an ω-Jónsson function, named for Bjarni Jónsson
Bjarni Jónsson
Bjarni Jónsson is an Icelandic mathematician and logician working in universal algebra and lattice theory. He is emeritus Distinguished Professor of Mathematics at Vanderbilt University and the honorary editor in chief of Algebra Universalis...
, for a set of ordinals x is a function from
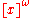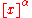to x such that for any subset y of x with the same cardinality as x, f restricted to maps onto x. Here if x is an ordered set and α is an ordinal, is the set of subsets of x of order type α. So in particular is the set of strictly increasing sequences of x.showed that for any ordinal λ there is an ω-Jónsson function for λ.
Kunen's proof of Kunen's inconsistency theorem
Kunen's inconsistency theorem
In set theory, a branch of mathematics, Kunen's inconsistency theorem, proved by , shows that several plausible large cardinal axioms are inconsistent with the axiom of choice.Some consequences of Kunen's theorem are:...
uses a Jónsson function for cardinals λ such that 2λ = λℵ0, and Kunen observed that for this special case there is a simpler proof of the existence of Jónsson functions. gave a simple proof for the general case.
The existence of Jónsson functions shows that for any cardinal there is an algebra with an infinitary operation that has no proper subalgebras of the same cardinality. In particular if infinitary operations are allowed then an analogue of Jónsson algebras exists in any cardinality, so there are no infinitary analogues of Jónsson cardinal
Jónsson cardinal
In set theory, a Jónsson cardinal is a certain kind of large cardinal number.An uncountable cardinal number κ is said to be Jónsson if for every function f: [κ]...
s.