Kaiser window
Encyclopedia
The Kaiser window is a one-parameter family of window function
s used for digital signal processing
, and is defined by the formula
:
where:
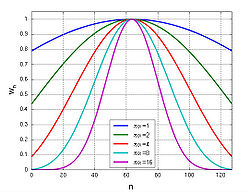
When N is an odd number, the peak value of the window is wM/2 = 1. And when N is even, the peak values are wN/2-1 = wN/2 < 1.
Window function
In signal processing, a window function is a mathematical function that is zero-valued outside of some chosen interval. For instance, a function that is constant inside the interval and zero elsewhere is called a rectangular window, which describes the shape of its graphical representation...
s used for digital signal processing
Digital signal processing
Digital signal processing is concerned with the representation of discrete time signals by a sequence of numbers or symbols and the processing of these signals. Digital signal processing and analog signal processing are subfields of signal processing...
, and is defined by the formula
:
where:
- I0 is the zeroth order Modified Bessel function of the first kind.
- α is an arbitrary real number that determines the shape of the window. In the frequency domain, it determines the trade-off between main-lobe width and side lobe level, which is a central decision in window design.
- M is an integer, and the length of the sequence is N=M+1.
When N is an odd number, the peak value of the window is wM/2 = 1. And when N is even, the peak values are wN/2-1 = wN/2 < 1.
Frequency response
Underlying the discrete sequence is this continuous-time function and its Fourier transform:-
-
The maximum value of w(t) is w(0) = 1. The wn sequence defined above are the samples of:
for all integer values of t,
and where rect is the rectangle function.
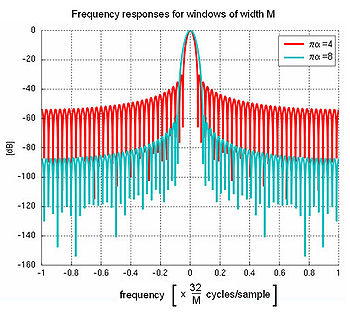
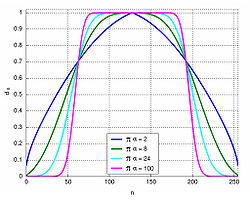
The larger the value of |α|, the narrower the window becomes; α = 0 corresponds to a rectangular window. Conversely, for larger |α| the main lobe of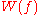
increases in width, while the side lobes decrease in amplitude. Thus, this parameter controls the tradeoff between main-lobe width and side-lobe area, as is illustrated in the plot of the frequency spectra below. For large α, the shape of the Kaiser window (in both time and frequency domain) tends to a Gaussian curve. The Kaiser window is nearly optimal in the sense of its peak's concentration around ω = 0 (Oppenheim et al., 1999).
Kaiser-Bessel derived (KBD) window
A related window function is the Kaiser-Bessel derived (KBD) window, which is designed to be suitable for use with the modified discrete cosine transformModified discrete cosine transformThe modified discrete cosine transform is a Fourier-related transform based on the type-IV discrete cosine transform , with the additional property of being lapped: it is designed to be performed on consecutive blocks of a larger dataset,...
(MDCT). The KBD window function is defined in terms of the Kaiser window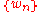
of length M+1, by the formula:
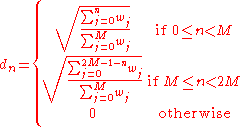
This defines a window of length 2M, where by construction dn satisfies the Princen-Bradley condition for the MDCT (using the fact that wM−n = wn): dn2 + dn + M2 = 1 (interpreting n and n + M moduloModular arithmeticIn mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
2M). The KBD window is also symmetric in the proper manner for the MDCT: dn = d2M−1−n.
-