Kaplan-Meier estimator
Encyclopedia
The Kaplan–Meier estimator, also known as the product limit estimator, is an estimator
for estimating the survival function
from life-time data. In medical research, it is often used to measure the fraction of patients living for a certain amount of time after treatment. In economics, it can be used to measure the length of time people remain unemployed after a job loss. In engineering, it can be used to measure the time until failure of machine parts. In ecology, it can be used to estimate how long fleshy fruits remain on plants before they are removed by frugivores. The estimator is named after Edward L. Kaplan and Paul Meier
.
A plot of the Kaplan–Meier estimate of the survival function is a series of horizontal steps of declining magnitude which, when a large enough sample is taken, approaches the true survival function for that population. The value of the survival function between successive distinct sampled observations ("clicks") is assumed to be constant.
An important advantage of the Kaplan–Meier curve is that the method can take into account some types of censored data
, particularly right-censoring, which occurs if a patient withdraws from a study, i.e. is lost from the sample before the final outcome is observed. On the plot, small vertical tick-marks indicate losses, where a patient's survival time has been right-censored. When no truncation or censoring occurs, the Kaplan–Meier curve is equivalent to the empirical distribution function
.
In medical statistics
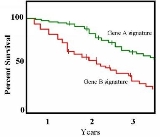
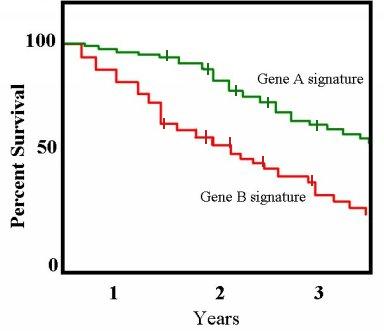
, a typical application might involve grouping patients into categories, for instance, those with Gene A profile and those with Gene B profile. In the graph, patients with Gene B die much more quickly than those with gene A. After two years, about 80% of the Gene A patients survive, but less than half of patients with Gene B.
Corresponding to each ti is ni, the number "at risk" just prior to time ti, and di, the number of deaths at time ti.
Note that the intervals between each time typically are not uniform. For example, a small data set might begin with 10 cases, have a death at Day 3, a loss (censored case) at Day 9, and another death at Day 11. Then we have (t1 = 3, t2 = 11), (n1 = 10, n2 = 8), and (d1 = 1, d2 = 1).
The Kaplan–Meier estimator is the nonparametric maximum likelihood estimate of S(t). It is a product of the form
When there is no censoring, ni is just the number of survivors just prior to time ti. With censoring, ni is the number of survivors less the number of losses (censored cases). It is only those surviving cases that are still being observed (have not yet been censored) that are "at risk" of an (observed) death.
There is an alternative definition that is sometimes used, namely
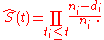
The two definitions differ only at the observed event times. The latter definition is right-continuous whereas the former definition is left-continuous.
Let T be the random variable that measures the time of failure and let F(t) be its cumulative distribution function
. Note that
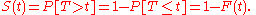
Consequently, the right-continuous definition of
may be preferred in order to make the estimate compatible with a right-continuous estimate of F(t).
, and several estimators are used to approximate its variance
. One of the most common such estimators is Greenwood's formula:
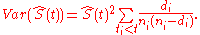
In some cases, one may wish to compare different Kaplan–Meier curves. This may be done by several methods including:
Estimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
for estimating the survival function
Survival function
The survival function, also known as a survivor function or reliability function, is a property of any random variable that maps a set of events, usually associated with mortality or failure of some system, onto time. It captures the probability that the system will survive beyond a specified time...
from life-time data. In medical research, it is often used to measure the fraction of patients living for a certain amount of time after treatment. In economics, it can be used to measure the length of time people remain unemployed after a job loss. In engineering, it can be used to measure the time until failure of machine parts. In ecology, it can be used to estimate how long fleshy fruits remain on plants before they are removed by frugivores. The estimator is named after Edward L. Kaplan and Paul Meier
Paul Meier (statistician)
Paul Meier was a statistician who promoted the use of randomized trials in medicine. He is also known for introducing, with Edward L. Kaplan, the Kaplan–Meier estimator, a tool for measuring how many patients survive a medical treatment.-External links:...
.
A plot of the Kaplan–Meier estimate of the survival function is a series of horizontal steps of declining magnitude which, when a large enough sample is taken, approaches the true survival function for that population. The value of the survival function between successive distinct sampled observations ("clicks") is assumed to be constant.
Censoring (statistics)
In statistics, engineering, and medical research, censoring occurs when the value of a measurement or observation is only partially known.For example, suppose a study is conducted to measure the impact of a drug on mortality. In such a study, it may be known that an individual's age at death is at...
, particularly right-censoring, which occurs if a patient withdraws from a study, i.e. is lost from the sample before the final outcome is observed. On the plot, small vertical tick-marks indicate losses, where a patient's survival time has been right-censored. When no truncation or censoring occurs, the Kaplan–Meier curve is equivalent to the empirical distribution function
Empirical distribution function
In statistics, the empirical distribution function, or empirical cdf, is the cumulative distribution function associated with the empirical measure of the sample. This cdf is a step function that jumps up by 1/n at each of the n data points. The empirical distribution function estimates the true...
.
In medical statistics
Medical statistics
Medical statistics deals with applications of statistics to medicine and the health sciences, including epidemiology, public health, forensic medicine, and clinical research...
, a typical application might involve grouping patients into categories, for instance, those with Gene A profile and those with Gene B profile. In the graph, patients with Gene B die much more quickly than those with gene A. After two years, about 80% of the Gene A patients survive, but less than half of patients with Gene B.
Formulation
Let S(t) be the probability that an item from a given population will have a lifetime exceeding t. For a sample from this population of size N let the observed times until death of N sample members beCorresponding to each ti is ni, the number "at risk" just prior to time ti, and di, the number of deaths at time ti.
Note that the intervals between each time typically are not uniform. For example, a small data set might begin with 10 cases, have a death at Day 3, a loss (censored case) at Day 9, and another death at Day 11. Then we have (t1 = 3, t2 = 11), (n1 = 10, n2 = 8), and (d1 = 1, d2 = 1).
The Kaplan–Meier estimator is the nonparametric maximum likelihood estimate of S(t). It is a product of the form
When there is no censoring, ni is just the number of survivors just prior to time ti. With censoring, ni is the number of survivors less the number of losses (censored cases). It is only those surviving cases that are still being observed (have not yet been censored) that are "at risk" of an (observed) death.
There is an alternative definition that is sometimes used, namely
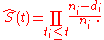
The two definitions differ only at the observed event times. The latter definition is right-continuous whereas the former definition is left-continuous.
Let T be the random variable that measures the time of failure and let F(t) be its cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
. Note that
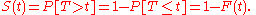
Consequently, the right-continuous definition of
may be preferred in order to make the estimate compatible with a right-continuous estimate of F(t).Statistical considerations
The Kaplan–Meier estimator is a statisticStatistic
A statistic is a single measure of some attribute of a sample . It is calculated by applying a function to the values of the items comprising the sample which are known together as a set of data.More formally, statistical theory defines a statistic as a function of a sample where the function...
, and several estimators are used to approximate its variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
. One of the most common such estimators is Greenwood's formula:
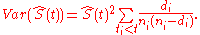
In some cases, one may wish to compare different Kaplan–Meier curves. This may be done by several methods including:
- The log rank test
- The Cox proportional hazards testProportional hazards modelsProportional hazards models are a class of survival models in statistics. Survival models relate the time that passes before some event occurs to one or more covariates that may be associated with that quantity. In a proportional hazards model, the unique effect of a unit increase in a covariate...