
Kaplansky density theorem
Encyclopedia
In the theory of von Neumann algebra
s, the Kaplansky density theorem states that
if A is a *-subalgebra of the algebra B(H) of bounded operators on a Hilbert space
H, then the strong closure of the unit ball of A in B(H) is the unit ball of the strong closure of A in B(H). This gives a strengthening of the von Neumann bicommutant theorem
, showing that an element a of the double commutant of A, denoted by A′′, can be strongly approximated by elements of A whose norm is no larger than that of a.
The standard proof uses the fact that, when f is bounded, the continuous functional calculus
a f(a) satisfies, for a net {aα} of self adjoint operators
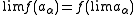
in the strong operator topology
. This shows that self-adjoint part of the unit ball in A′′ can be approximated strongly by self-adjoint elements in the C*-algebra generated by A. A matrix computation then removes the self-adjointness restriction and proves the theorem.
Von Neumann algebra
In mathematics, a von Neumann algebra or W*-algebra is a *-algebra of bounded operators on a Hilbert space that is closed in the weak operator topology and contains the identity operator. They were originally introduced by John von Neumann, motivated by his study of single operators, group...
s, the Kaplansky density theorem states that
if A is a *-subalgebra of the algebra B(H) of bounded operators on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
H, then the strong closure of the unit ball of A in B(H) is the unit ball of the strong closure of A in B(H). This gives a strengthening of the von Neumann bicommutant theorem
Von Neumann bicommutant theorem
In mathematics, specifically functional analysis, the von Neumann bicommutant theorem relates the closure of a set of bounded operators on a Hilbert space in certain topologies to the bicommutant of that set. In essence, it is a connection between the algebraic and topological sides of operator...
, showing that an element a of the double commutant of A, denoted by A′′, can be strongly approximated by elements of A whose norm is no larger than that of a.
The standard proof uses the fact that, when f is bounded, the continuous functional calculus
Continuous functional calculus
In mathematics, the continuous functional calculus of operator theory and C*-algebra theory allows applications of continuous functions to normal elements of a C*-algebra. More precisely,Theorem...
a f(a) satisfies, for a net {aα} of self adjoint operators
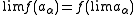
in the strong operator topology
Strong operator topology
In functional analysis, a branch of mathematics, the strong operator topology, often abbreviated SOT, is the weakest locally convex topology on the set of bounded operators on a Hilbert space such that the evaluation map sending an operator T to the real number \|Tx\| is continuous for each vector...
. This shows that self-adjoint part of the unit ball in A′′ can be approximated strongly by self-adjoint elements in the C*-algebra generated by A. A matrix computation then removes the self-adjointness restriction and proves the theorem.

