
Kappa calculus
Encyclopedia
In mathematical logic
, category theory
, and
computer science
, kappa calculus is a
formal system
for defining first-order
functions
.
Unlike lambda calculus
, kappa calculus has no
higher-order functions
; its functions are
not first class objects
. Kappa-calculus can be
regarded as "a reformulation of the first-order fragment of typed
lambda calculus".
Because its functions are not first-class objects, evaluation of kappa
calculus expressions does not require
closures
.
and 207 of Hasegawa.
grammar below:

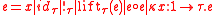
In other words,
The and the subscripts of id, !, and
and the subscripts of id, !, and 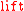 are
are
sometimes omitted when they can be unambiguously determined from the
context.
Juxtaposition is often used as an abbreviation for a combination of
"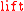 " and composition:
" and composition:
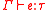 ) rather than hypothetical judgments in order to ease comparison with the simply typed lambda calculus. This requires the additional Var rule, which does not appear in Hasegawa
) rather than hypothetical judgments in order to ease comparison with the simply typed lambda calculus. This requires the additional Var rule, which does not appear in Hasegawa
In kappa calculus an expression has two types: the type of its source and the type of its target. The notation is used to indicate that expression e has source type
is used to indicate that expression e has source type 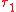 and target type
and target type 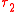 .
.
Expressions in kappa calculus are assigned types according to the following rules:
In other words,
The last two equalities are reduction rules for the calculus,
rewriting from left to right.
. Because of this, any two functions whose argument type is the same and whose result type is 1 should be equal – since there is only a single value of type 1 both functions must return that value for every argument (Terminality).
Expressions with type can be regarded as "constants" or values of "ground type"; this is because 1 is the unit type, and so a function from this type is necessarily a constant function. Note that the kappa rule allows abstractions only when the variable being abstracted has the type
can be regarded as "constants" or values of "ground type"; this is because 1 is the unit type, and so a function from this type is necessarily a constant function. Note that the kappa rule allows abstractions only when the variable being abstracted has the type  for some
for some  . This is the basic mechanism which ensures that all functions are first-order.
. This is the basic mechanism which ensures that all functions are first-order.
contextually complete categories.
"right-imbalanced" binary trees. For example, a function f with three
arguments of types A, B, and C and result type D will have type
If we define left-associative juxtaposition (f c) as an abbreviation
for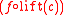 , then – assuming that
, then – assuming that
 ,
,  , and
, and
 – we can apply this function:
– we can apply this function:
Since the expression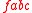 has source type 1, it is a "ground value" and may be passed as an argument to another function. If
has source type 1, it is a "ground value" and may be passed as an argument to another function. If 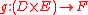 , then
, then
Much like a curried function of type
 in lambda calculus, partial
in lambda calculus, partial
application is possible:
However no higher types (i.e.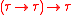 ) are involved. Note that because the source type of
) are involved. Note that because the source type of 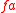 is not 1, the following expression cannot be well-typed under the assumptions mentioned so far:
is not 1, the following expression cannot be well-typed under the assumptions mentioned so far:
Because successive application is used for multiple
arguments it is not necessary to know the arity
of a function in
order to determine its typing; for example, if we know that
 then the expression
then the expression
is well-typed as long as j has type
 for some
for some 
and . This property is important when calculating
. This property is important when calculating
the principal type
of an expression, something
which can be difficult when attempting to exclude higher-order
functions from typed lambda calculi by restricting the grammar of types.
"functional completeness" in the context of combinatory algebra.
Kappa calculus arose out of efforts by Lambek
completeness for arbitrary categories (see Hermida and Jacobs
calculus into a usable (though simple) programming language including
arithmetic over natural numbers and primitive recursion
were later investigated by Power, Thielecke, and others.
substructural types
such as linear
, affine
,
and ordered
types. These extensions require eliminating or
restricting the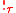 expression. In such circumstances
expression. In such circumstances
the type operator is not a true cartesian product,
type operator is not a true cartesian product,
and is generally written to make this clear.
to make this clear.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, and
computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, kappa calculus is a
formal system
Formal system
In formal logic, a formal system consists of a formal language and a set of inference rules, used to derive an expression from one or more other premises that are antecedently supposed or derived . The axioms and rules may be called a deductive apparatus...
for defining first-order
functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
.
Unlike lambda calculus
Lambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
, kappa calculus has no
higher-order functions
Higher-order function
In mathematics and computer science, higher-order functions, functional forms, or functionals are functions which do at least one of the following:*take one or more functions as an input*output a function...
; its functions are
not first class objects
First-class object
In programming language design, a first-class citizen , in the context of a particular programming language, is an entity that can be constructed at run-time, passed as a parameter, returned from a subroutine, or assigned into a variable...
. Kappa-calculus can be
regarded as "a reformulation of the first-order fragment of typed
lambda calculus".
Because its functions are not first-class objects, evaluation of kappa
calculus expressions does not require
closures
Closure (computer science)
In computer science, a closure is a function together with a referencing environment for the non-local variables of that function. A closure allows a function to access variables outside its typical scope. Such a function is said to be "closed over" its free variables...
.
Definition
The definition below has been adapted from the diagrams on pages 205and 207 of Hasegawa.
Grammar
Kappa calculus consists of types and expressions, given by thegrammar below:

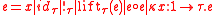
In other words,
- 1 is a type
- If
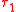 and
and  are types then
are types then  is a type.
is a type. - Every variable is an expression
- If
 is a type then
is a type then 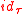 is an expression
is an expression - If
 is a type then
is a type then  is an expression
is an expression - If
 is a type and e is an expression then
is a type and e is an expression then 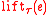 is an expression
is an expression - If
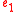 and
and  are expressions then
are expressions then  is an expression
is an expression - If x is a variable,
 is a type, and e is an expression, then
is a type, and e is an expression, then  is an expression
is an expression
The
 and the subscripts of id, !, and
and the subscripts of id, !, and 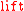 are
aresometimes omitted when they can be unambiguously determined from the
context.
Juxtaposition is often used as an abbreviation for a combination of
"
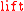 " and composition:
" and composition:Typing rules
The presentation here uses sequents (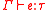 ) rather than hypothetical judgments in order to ease comparison with the simply typed lambda calculus. This requires the additional Var rule, which does not appear in Hasegawa
) rather than hypothetical judgments in order to ease comparison with the simply typed lambda calculus. This requires the additional Var rule, which does not appear in HasegawaIn kappa calculus an expression has two types: the type of its source and the type of its target. The notation
 is used to indicate that expression e has source type
is used to indicate that expression e has source type 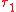 and target type
and target type 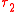 .
.Expressions in kappa calculus are assigned types according to the following rules:
In other words,
- Var: assuming
 lets you conclude that
lets you conclude that 
- Id: for any type
 ,
, 
- Bang: for any type
 ,
, 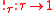
- Comp: if the target type of
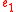 matches the source type of
matches the source type of 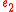 they may be composed to form an expression
they may be composed to form an expression 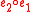 with the source type of
with the source type of 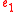 and target type of
and target type of 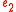
- Lift: if
 , then
, then 
- Kappa: if we can conclude that
 under the assumption that
under the assumption that  , then we may conclude without that assumption that
, then we may conclude without that assumption that 
Equalities
Kappa calculus obeys the following equalities:- Neutrality: If
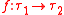 then
then  and
and 
- Associativity: If
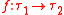 ,
,  , and
, and  , then
, then 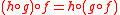 .
. - Terminality: If
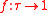 and
and 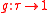 then
then 
- Lift-Reduction:
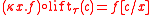
- Kappa-Reduction:
 if x is not free in h
if x is not free in h
The last two equalities are reduction rules for the calculus,
rewriting from left to right.
Properties
The type 1 can be regarded as the unit typeUnit type
In the area of mathematical logic, and computer science known as type theory, a unit type is a type that allows only one value . The carrier associated with a unit type can be any singleton set. There is an isomorphism between any two such sets, so it is customary to talk about the unit type and...
. Because of this, any two functions whose argument type is the same and whose result type is 1 should be equal – since there is only a single value of type 1 both functions must return that value for every argument (Terminality).
Expressions with type
 can be regarded as "constants" or values of "ground type"; this is because 1 is the unit type, and so a function from this type is necessarily a constant function. Note that the kappa rule allows abstractions only when the variable being abstracted has the type
can be regarded as "constants" or values of "ground type"; this is because 1 is the unit type, and so a function from this type is necessarily a constant function. Note that the kappa rule allows abstractions only when the variable being abstracted has the type  for some
for some  . This is the basic mechanism which ensures that all functions are first-order.
. This is the basic mechanism which ensures that all functions are first-order.Categorical semantics
Kappa calculus is intended to be the internal language ofcontextually complete categories.
Examples
Expressions with multiple arguments have source types which are"right-imbalanced" binary trees. For example, a function f with three
arguments of types A, B, and C and result type D will have type
If we define left-associative juxtaposition (f c) as an abbreviation
for
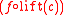 , then – assuming that
, then – assuming that ,
,  , and
, and – we can apply this function:
– we can apply this function:Since the expression
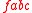 has source type 1, it is a "ground value" and may be passed as an argument to another function. If
has source type 1, it is a "ground value" and may be passed as an argument to another function. If 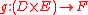 , then
, thenMuch like a curried function of type
 in lambda calculus, partial
in lambda calculus, partialapplication is possible:
However no higher types (i.e.
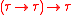 ) are involved. Note that because the source type of
) are involved. Note that because the source type of 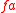 is not 1, the following expression cannot be well-typed under the assumptions mentioned so far:
is not 1, the following expression cannot be well-typed under the assumptions mentioned so far:Because successive application is used for multiple
arguments it is not necessary to know the arity
Arity
In logic, mathematics, and computer science, the arity of a function or operation is the number of arguments or operands that the function takes. The arity of a relation is the dimension of the domain in the corresponding Cartesian product...
of a function in
order to determine its typing; for example, if we know that
 then the expression
then the expressionis well-typed as long as j has type
 for some
for some 
and
 . This property is important when calculating
. This property is important when calculatingthe principal type
Principal type
In type theory, the principal type of an expression is the most general possible type given an expression. One way to compute the principal type of an expression is by deploying Robinson's unification algorithm, which is used by the Hindley–Milner type inference algorithm.Expressions always...
of an expression, something
which can be difficult when attempting to exclude higher-order
functions from typed lambda calculi by restricting the grammar of types.
History
Barendregt originally introduced the term"functional completeness" in the context of combinatory algebra.
Kappa calculus arose out of efforts by Lambek
completeness for arbitrary categories (see Hermida and Jacobs
calculus into a usable (though simple) programming language including
arithmetic over natural numbers and primitive recursion
were later investigated by Power, Thielecke, and others.
Variants
It is possible to explore versions of kappa calculus withsubstructural types
Substructural logic
In logic, a substructural logic is a logic lacking one of the usual structural rules , such as weakening, contraction or associativity...
such as linear
Linear type system
A linear type system is a particular form of type system used in a programming language. Linear type systems allow references but not aliases. To enforce this, a reference goes out of scope after appearing on the right-hand side of an assignment, thus ensuring that only one reference to any object...
, affine
Affine logic
Affine logic is a substructural logic whose proof theory rejects the structural rule of contraction. It can also be characterized as linear logic with weakening....
,
and ordered
Noncommutative logic
Noncommutative logic is an extension of linear logic which combines the commutative connectives of linear logic with the noncommutative multiplicative connectives of the Lambek calculus...
types. These extensions require eliminating or
restricting the
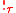 expression. In such circumstances
expression. In such circumstancesthe
 type operator is not a true cartesian product,
type operator is not a true cartesian product,and is generally written
 to make this clear.
to make this clear.

