Karger's algorithm
Encyclopedia
In computer science
and graph theory
, the Karger's algorithm is a Monte Carlo method
to compute the minimum cut
of a connected graph
developed by David Karger
.
in a graph. Informally speaking, the contraction of an edge makes the two nodes joined by e overlap, reducing the total number of nodes of the graph by one. The algorithm proceeds iterating contractions until only two nodes are left in the graph. With high probability, the algorithm will return a minimal cut by returning the set of edges joining the two remaining nodes.
Karger's algorithm
is the fastest known minimum cut algorithm, is randomized, and computes a minimum cut with high probability in time O(|E| log3|V|).
with endpoints 
and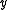 
and contracts it into a new node 
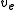which becomes adjacent to all former neighbors of 
and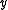 
. It is possible to formalize this concept in mathematical terms.
Given a graph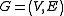
and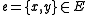 
, the contraction of 
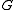respect to 
(written 
) is a multigraph
where:
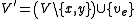
and:
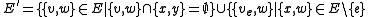or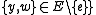 
It is possible to prove that this operation doesn't reduce the cardinality of the minimum cut, but that it might increase it.
function Karger(G, K)
min :=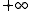
for i = 1 to K do
t := Full_contraction(G)
if t < min then
min := t
return min
function Full_contraction(G)
for i := 1 to |V| - 2 do
e := Random(
)
G' = ( V',
') := 
V := V'
:= 
'
return |
|
The function Full_contraction implements the contraction of the edges following the given definition. The iteration lasts until only two nodes are left in the graph. With a certain probability, the set of edges left are the minimum cut.
It is not sure anyway that this algorithm returns a cut which is minimum, therefore K execution of Full_contraction is performed by the Karger function, where K has to be passed as a parameter. Computing the minimum of the K executions reduces the probability of having a wrong minimum cut returned.
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
and graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the Karger's algorithm is a Monte Carlo method
Monte Carlo method
Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
to compute the minimum cut
Minimum cut
In graph theory, a minimum cut of a graph is a cut whose cutset has the smallest number of elements or smallest sum of weights possible...
of a connected graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
developed by David Karger
David Karger
David Karger is a Professor of Computer Science and a member of the Computer Science and Artificial Intelligence Laboratory at the Massachusetts Institute of Technology . He received an AB from Harvard University and a PhD in computer science from Stanford University. Dr...
.
Algorithm
The idea of the algorithm is based on the concept of contraction of an edge in a graph. Informally speaking, the contraction of an edge makes the two nodes joined by e overlap, reducing the total number of nodes of the graph by one. The algorithm proceeds iterating contractions until only two nodes are left in the graph. With high probability, the algorithm will return a minimal cut by returning the set of edges joining the two remaining nodes.Karger's algorithm
Karger's algorithm
In computer science and graph theory, the Karger's algorithm is a Monte Carlo method to compute the minimum cut of a connected graph developed by David Karger.-Algorithm:The idea of the algorithm is based on the concept of contraction of an edge e in a graph...
is the fastest known minimum cut algorithm, is randomized, and computes a minimum cut with high probability in time O(|E| log3|V|).
Contraction
Informally speaking, this operation takes an edge with endpoints and 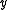and contracts it into a new node 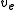which becomes adjacent to all former neighbors of and 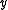. It is possible to formalize this concept in mathematical terms.Given a graph
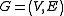and 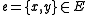, the contraction of 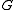respect to (written ) is a multigraphMultigraph
In mathematics, a multigraph or pseudograph is a graph which is permitted to have multiple edges, , that is, edges that have the same end nodes. Thus two vertices may be connected by more than one edge....
where:
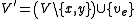
and:
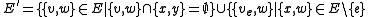or 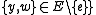It is possible to prove that this operation doesn't reduce the cardinality of the minimum cut, but that it might increase it.
Pseudocode
The algorithm can be implemented using two functions:function Karger(G, K)
min :=
for i = 1 to K do
t := Full_contraction(G)
if t < min then
min := t
return min
function Full_contraction(G)
for i := 1 to |V| - 2 do
e := Random(
)G' = ( V',
') := V := V'
:= 'return |
|The function Full_contraction implements the contraction of the edges following the given definition. The iteration lasts until only two nodes are left in the graph. With a certain probability, the set of edges left are the minimum cut.
It is not sure anyway that this algorithm returns a cut which is minimum, therefore K execution of Full_contraction is performed by the Karger function, where K has to be passed as a parameter. Computing the minimum of the K executions reduces the probability of having a wrong minimum cut returned.