In computer science

Computer science

Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...

, a k-d tree (short for k-dimensional tree) is a space-partitioning

Space partitioning

In mathematics, space partitioning is the process of dividing a space into two or more disjoint subsets . In other words, space partitioning divides a space into non-overlapping regions...

 data structure

Data structure

In computer science, a data structure is a particular way of storing and organizing data in a computer so that it can be used efficiently.Different kinds of data structures are suited to different kinds of applications, and some are highly specialized to specific tasks...

 for organizing point

Point (geometry)

In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...

s in a k-dimensional space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

. k-d trees are a useful data structure for several applications, such as searches involving a multidimensional search key (e.g. range searches and nearest neighbor search

Nearest neighbor search

Nearest neighbor search , also known as proximity search, similarity search or closest point search, is an optimization problem for finding closest points in metric spaces. The problem is: given a set S of points in a metric space M and a query point q ∈ M, find the closest point in S to q...

es). k-d trees are a special case of binary space partitioning

Binary space partitioning

In computer science, binary space partitioning is a method for recursively subdividing a space into convex sets by hyperplanes. This subdivision gives rise to a representation of the scene by means of a tree data structure known as a BSP tree.Originally, this approach was proposed in 3D computer...

 trees.

Informal description

The k-d tree is a binary tree

Binary tree

In computer science, a binary tree is a tree data structure in which each node has at most two child nodes, usually distinguished as "left" and "right". Nodes with children are parent nodes, and child nodes may contain references to their parents. Outside the tree, there is often a reference to...

 in which every node is a k-dimensional point. Every non-leaf node can be thought of as implicitly generating a splitting hyperplane

Hyperplane

A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...

 that divides the space into two parts, known as subspaces. Points to the left of this hyperplane represent the left subtree of that node and points right of the hyperplane are represented by the right subtree. The hyperplane direction is chosen in the following way: every node in the tree is associated with one of the k-dimensions, with the hyperplane perpendicular to that dimension's axis. So, for example, if for a particular split the "x" axis is chosen, all points in the subtree with a smaller "x" value than the node will appear in the left subtree and all points with larger "x" value will be in the right subtree. In such a case, the hyperplane would be set by the x-value of the point, and its normal

Surface normal

A surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...

 would be the unit x-axis.

Construction

Since there are many possible ways to choose axis-aligned splitting planes, there are many different ways to construct k-d trees. The canonical method of k-d tree construction has the following constraints:

• As one moves down the tree, one cycles through the axes used to select the splitting planes. (For example, in a 3-dimensional tree, the root would have an x-aligned plane, the root's children would both have y-aligned planes, the root's grandchildren would all have z-aligned planes, the next level would have an x-aligned plane, and so on.)
• Points are inserted by selecting the median
  Median
  In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
  
   of the points being put into the subtree, with respect to their coordinates in the axis being used to create the splitting plane. (Note the assumption that we feed the entire set of points into the algorithm up-front.)

This method leads to a balanced k-d tree, in which each leaf node is about the same distance from the root. However, balanced trees are not necessarily optimal for all applications.

Note also that it is not required to select the median point. In that case, the result is simply that there is no guarantee that the tree will be balanced. A simple heuristic to avoid coding a complex linear-time median-finding algorithm or using an O(n log n) sort is to use sort to find the median of a fixed number of randomly selected points to serve as the cut line. Practically this technique often results in nicely balanced trees.

Given a list of n points, the following algorithm

Algorithm

In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...

 will construct a balanced k-d tree containing those points.

function kdtree (list of points pointList, int depth)
{
if pointList is empty
return nil;
else
{
// Select axis based on depth so that axis cycles through all valid values
var int axis := depth mod k;

// Sort point list and choose median as pivot element
select

Selection algorithm

In computer science, a selection algorithm is an algorithm for finding the kth smallest number in a list . This includes the cases of finding the minimum, maximum, and median elements. There are O, worst-case linear time, selection algorithms...

 median by axis from pointList;

// Create node and construct subtrees
var tree_node node;
node.location := median;
node.leftChild := kdtree(points in pointList before median, depth+1);
node.rightChild := kdtree(points in pointList after median, depth+1);
return node;
}
}
It is common that points "after" the median include only the ones that are strictly greater than the median. Another approach is to define a "superkey" function that compares the points in other dimensions. Lastly, it may be acceptable to let points equal to the median lie on either side.

This algorithm implemented in the Python programming language

Python (programming language)

Python is a general-purpose, high-level programming language whose design philosophy emphasizes code readability. Python claims to "[combine] remarkable power with very clear syntax", and its standard library is large and comprehensive...

 is as follows:


class Node: pass

def kdtree(point_list, depth=0):
if not point_list:
return

# Select axis based on depth so that axis cycles through all valid values
k = len(point_list[0]) # assumes all points have the same dimension
axis = depth % k

# Sort point list and choose median as pivot element
point_list.sort(key=lambda point: point[axis])
median = len(point_list) // 2 # choose median

# Create node and construct subtrees
node = Node
node.location = point_list[median]
node.left_child = kdtree(point_list[:median], depth + 1)
node.right_child = kdtree(point_list[median + 1:], depth + 1)
return node


Example usage would be:

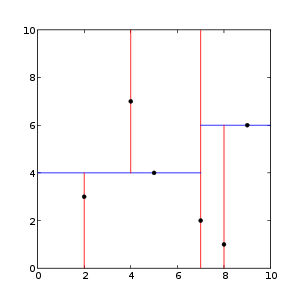
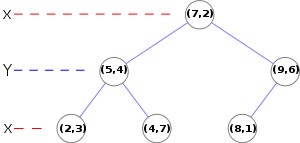
point_list = [(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)]
tree = kdtree(point_list)

The tree generated is shown on the right.

This algorithm creates the invariant

Invariant (computer science)

In computer science, a predicate is called an invariant to a sequence of operations provided that: if the predicate is true before starting the sequence, then it is true at the end of the sequence.-Use:...

 that for any node, all the nodes in the left subtree are on one side of a splitting plane

Plane (mathematics)

In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...

, and all the nodes in the right subtree are on the other side. Points that lie on the splitting plane may appear on either side. The splitting plane of a node goes through the point associated with that node (referred to in the code as node.location).

Adding elements

One adds a new point to a k-d tree in the same way as one adds an element to any other search tree

Binary search tree

In computer science, a binary search tree , which may sometimes also be called an ordered or sorted binary tree, is a node-based binary tree data structurewhich has the following properties:...

. First, traverse the tree, starting from the root and moving to either the left or the right child depending on whether the point to be inserted is on the "left" or "right" side of the splitting plane. Once you get to the node under which the child should be located, add the new point as either the left or right child of the leaf node, again depending on which side of the node's splitting plane contains the new node.

Adding points in this manner can cause the tree to become unbalanced, leading to decreased tree performance. The rate of tree performance degradation is dependent upon the spatial distribution of tree points being added, and the number of points added in relation to the tree size. If a tree becomes too unbalanced, it may need to be re-balanced to restore the performance of queries that rely on the tree balancing, such as nearest neighbour searching.

Removing elements

To remove a point from an existing k-d tree, without breaking the invariant, the easiest way is to form the set of all nodes and leaves from the children of the target node, and recreate that part of the tree.

Another approach is to find a replacement for the point removed. First, find the node R that contains the point to be removed. For the base case where R is a leaf node, no replacement is required. For the general case, find a replacement point, say p, from the subtree rooted at R. Replace the point stored at R with p. Then, recursively remove p.

For finding a replacement point, if R discriminates on x (say) and R has a right child, find the point with the minimum x value from the subtree rooted at the right child. Otherwise, find the point with the maximum x value from the subtree rooted at the left child.

Balancing

Balancing a k-d tree requires care. Because k-d trees are sorted in multiple dimensions, the tree rotation

Tree rotation

A tree rotation is an operation on a binary tree that changes the structure without interfering with the order of the elements. A tree rotation moves one node up in the tree and one node down...

 technique cannot be used to balance them — this may break the invariant.

Several variants of balanced k-d trees exist. They include divided k-d tree, pseudo k-d tree, k-d B-tree, hB-tree and Bkd-tree. Many of these variants are adaptive k-d tree

Adaptive k-d tree

An adaptive k-d tree is a tree for multidimensional points where successive levels may be split along different dimensions....

s.

Nearest neighbour search

The nearest neighbour search (NN) algorithm aims to find the point in the tree that is nearest to a given input point. This search can be done efficiently by using the tree properties to quickly eliminate large portions of the search space.

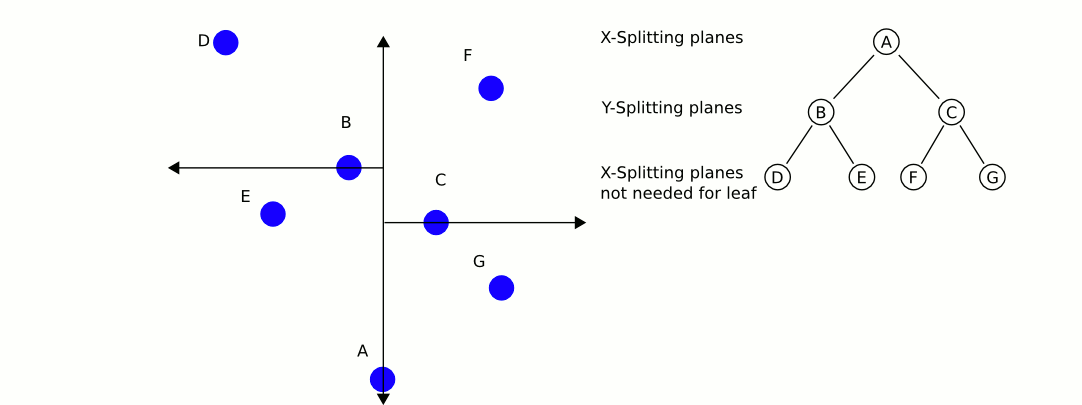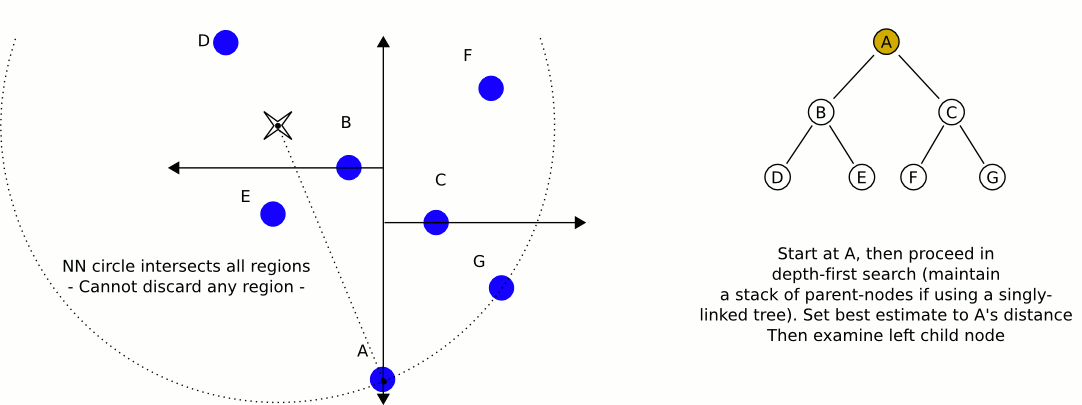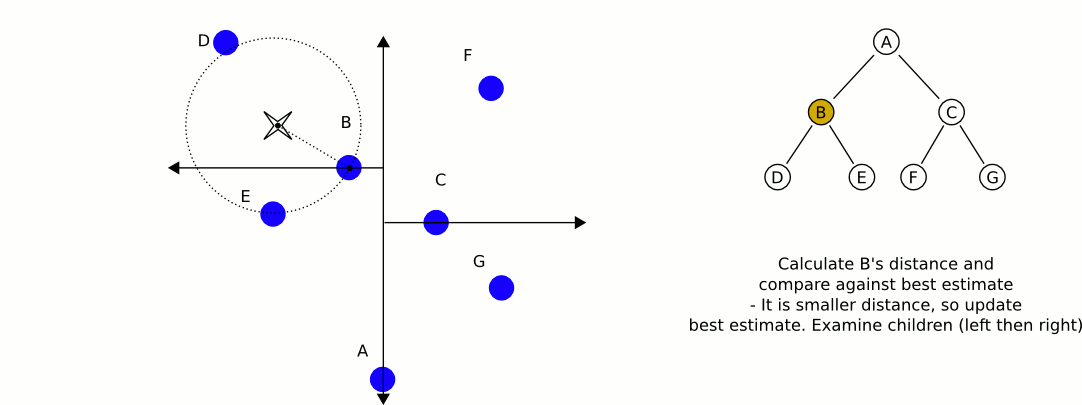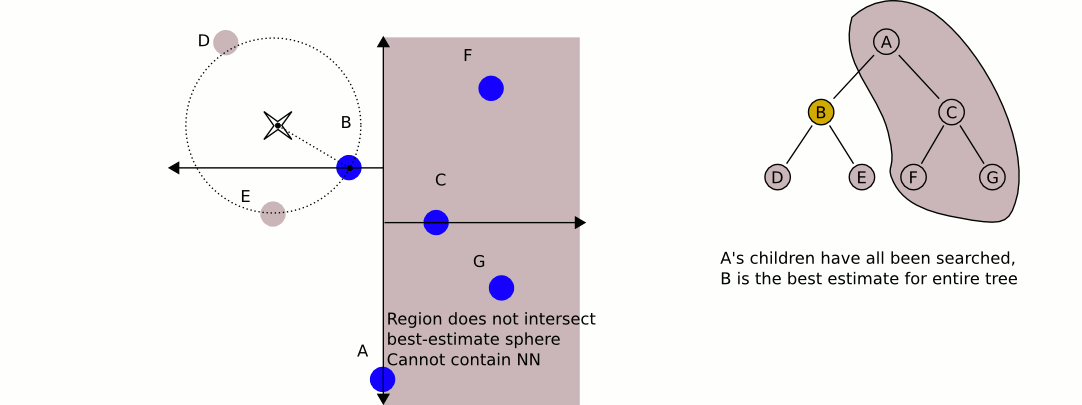
Searching for a nearest neighbour in a k-d tree proceeds as follows:

1. Starting with the root node, the algorithm moves down the tree recursively, in the same way that it would if the search point were being inserted (i.e. it goes left or right depending on whether the point is less than or greater than the current node in the split dimension).
2. Once the algorithm reaches a leaf node, it saves that node point as the "current best"
3. The algorithm unwinds the recursion of the tree, performing the following steps at each node:
   1. If the current node is closer than the current best, then it becomes the current best.
   2. The algorithm checks whether there could be any points on the other side of the splitting plane that are closer to the search point than the current best. In concept, this is done by intersecting the splitting hyperplane
      Hyperplane
      A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
      
       with a hypersphere
      Hypersphere
      In mathematics, an n-sphere is a generalization of the surface of an ordinary sphere to arbitrary dimension. For any natural number n, an n-sphere of radius r is defined as the set of points in -dimensional Euclidean space which are at distance r from a central point, where the radius r may be any...
      
       around the search point that has a radius equal to the current nearest distance. Since the hyperplanes are all axis-aligned this is implemented as a simple comparison to see whether the difference between the splitting coordinate of the search point and current node is less than the distance (overall coordinates) from the search point to the current best.
      1. If the hypersphere crosses the plane, there could be nearer points on the other side of the plane, so the algorithm must move down the other branch of the tree from the current node looking for closer points, following the same recursive process as the entire search.
      2. If the hypersphere doesn't intersect the splitting plane, then the algorithm continues walking up the tree, and the entire branch on the other side of that node is eliminated.
4. When the algorithm finishes this process for the root node, then the search is complete.

Generally the algorithm uses squared distances for comparison to avoid computing square roots. Additionally, it can save computation by holding the squared current best distance in a variable for comparison.

Finding the nearest point is an O(log N) operation in the case of randomly distributed points. Analyses of binary search trees has found that the worst case search time for a k-dimensional KD tree containing N nodes is given by the following equation.


In very high dimensional spaces, the curse of dimensionality

Curse of dimensionality

The curse of dimensionality refers to various phenomena that arise when analyzing and organizing high-dimensional spaces that do not occur in low-dimensional settings such as the physical space commonly modeled with just three dimensions.There are multiple phenomena referred to by this name in...

 causes the algorithm to need to visit many more branches than in lower dimensional spaces. In particular, when the number of points is only slightly higher than the number of dimensions, the algorithm is only slightly better than a linear search of all of the points.

The algorithm can be extended in several ways by simple modifications. It can provide the k-Nearest Neighbours to a point by maintaining k current bests instead of just one. Branches are only eliminated when they can't have points closer than any of the k current bests.

It can also be converted to an approximation algorithm to run faster. For example, approximate nearest neighbour searching can be achieved by simply setting an upper bound on the number points to examine in the tree, or by interrupting the search process based upon a real time clock (which may be more appropriate in hardware implementations). Nearest neighbour for points that are in the tree already can be achieved by not updating the refinement for nodes that give zero distance as the result, this has the downside of discarding points that are not unique, but are co-located with the original search point.

Approximate nearest neighbour is useful in real-time applications such as robotics due to the significant speed increase gained by not searching for the best point exhaustively. One of its implementations is best-bin-first search.

High-dimensional data

k-d trees are not suitable for efficiently finding the nearest neighbour in high dimensional spaces. As a general rule, if the dimensionality is k, the number of points in the data, N, should be N >> 2^k. Otherwise, when k-d trees are used with high-dimensional data, most of the points in the tree will be evaluated and the efficiency is no better than exhaustive search, and approximate nearest-neighbour methods are used instead.

Complexity

• Building a static k-d tree from n points takes O
  Big O notation
  In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
  
  (n log ² n) time if an O
  Big O notation
  In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
  
  (n log n) sort is used to compute the median at each level. The complexity is O
  Big O notation
  In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
  
  (n log n) if a linear median-finding
  Selection algorithm
  In computer science, a selection algorithm is an algorithm for finding the kth smallest number in a list . This includes the cases of finding the minimum, maximum, and median elements. There are O, worst-case linear time, selection algorithms...
  
   algorithm such as the one described in Cormen et al. is used.

• Inserting a new point into a balanced k-d tree takes O(log n) time.
• Removing a point from a balanced k-d tree takes O(log n) time.
• Querying an axis-parallel range in a balanced k-d tree takes O(n^1-1/k +m) time, where m is the number of the reported points, and k the dimension of the k-d tree.

Volumetric objects

Instead of points, a k-d tree can also contain rectangle

Rectangle

In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...

s or hyperrectangles. Thus range search becomes the problem of returning all rectangles intersecting the search rectangle. The tree is constructed the usual way with all the rectangles at the leaves. In an orthogonal range search, the opposite coordinate is used when comparing against the median. For example, if the current level is split along x_high, we check the x_low coordinate of the search rectangle. If the median is less than the x_low coordinate of the search rectangle, then no rectangle in the left branch can ever intersect with the search rectangle and so can be pruned. Otherwise both branches should be traversed. See also interval tree

Interval tree

In computer science, an interval tree is an ordered tree data structure to hold intervals. Specifically, it allows one to efficiently find all intervals that overlap with any given interval or point. It is often used for windowing queries, for example, to find all roads on a computerized map inside...

, which is a 1-dimensional special case.

Points only in leaves

It is also possible to define a k-d tree with points stored solely in leaves. This form of k-d tree allows a variety of split mechanics other than the standard median split. The midpoint splitting rule selects on the middle of the longest axis of the space being searched, regardless of the distribution of points. This guarantees that the aspect ratio will be at most 2:1, but the depth is dependent on the distribution of points. A variation, called sliding-midpoint, only splits on the middle if there are points on both sides of the split. Otherwise, it splits on point nearest to the middle. Maneewongvatana and Mount show that this offers "good enough" performance on common data sets.
Using sliding-midpoint, an approximate nearest neighbour query can be answered in .
Approximate range counting can be answered in with this method.

See also

• implicit k-d tree
  Implicit kd-tree
  An implicit k-d tree is a k-d tree defined implicitly above a rectilinear grid. Its split planes' positions and orientations are not given explicitly but implicitly by some recursive splitting-function defined on the hyperrectangles belonging to the tree's nodes...
  
  
• min/max k-d tree
  Min/max kd-tree
  A min/max kd-tree is a kd-tree with two scalar values - a minimum and a maximum - assigned to its nodes. The minimum/maximum of an inner node is equal the minimum/maximum of its children's minima/maxima.-Construction:...
  
  
• Quadtree
  Quadtree
  A quadtree is a tree data structure in which each internal node has exactly four children. Quadtrees are most often used to partition a two dimensional space by recursively subdividing it into four quadrants or regions. The regions may be square or rectangular, or may have arbitrary shapes. This...
  
  
• Octree
  Octree
  An octree is a tree data structure in which each internal node has exactly eight children. Octrees are most often used to partition a three dimensional space by recursively subdividing it into eight octants. Octrees are the three-dimensional analog of quadtrees. The name is formed from oct + tree,...
  
  
• R-tree
  R-tree
  R-trees are tree data structures used for spatial access methods, i.e., for indexing multi-dimensional information such as geographical coordinates, rectangles or polygons. The R-tree was proposed by Antonin Guttman in 1984 and has found significant use in both research and real-world applications...
  
  
• Bounding Interval Hierarchy
  Bounding interval hierarchy
  A bounding interval hierarchy is a partitioning data structure similar to that of bounding volume hierarchies or kd-trees. Bounding interval hierarchies can be used in high performance ray tracing and may be especially useful for dynamic scenes.The BIH itself is, however, not new...
  
  
• Nearest neighbour search
• Klee's measure problem
  Klee's measure problem
  In computational geometry, Klee's measure problem is the problem of determining how efficiently the measure of a union of rectangular ranges can be computed...
  
  

External links

• libkdtree++, an open-source STL-like implementation of k-d trees in C++.
• A tutorial on KD Trees
• FLANN and its fork nanoflann, efficient C++ implementations of k-d tree algorithms.
• kdtree A simple C library for working with KD-Trees
• K-D Tree Demo, Java applet
• libANN Approximate Nearest Neighbour Library includes a k-d tree implementation
• Caltech Large Scale Image Search Toolbox: a Matlab toolbox implementing randomized k-d tree for fast approximate nearest neighbour search, in addition to LSH
  Locality sensitive hashing
  Locality-sensitive hashing is a method of performing probabilistic dimension reduction of high-dimensional data. The basic idea is to hash the input items so that similar items are mapped to the same buckets with high probability .-Definition:An LSH family \mathcal F is defined fora...
  
  , Hierarchical K-Means, and Inverted File search algorithms.
• Heuristic Ray Shooting Algorithms, pp. 11 and after