
KeY
Encyclopedia
The KeY tool is used in formal verification
of Java
programs.It accepts both specifications written in JML
or OCL
to Java source files. These are transformed into theorems of dynamic logic
and then compared against program semantics which are likewise defined in terms of dynamic logic. KeY is significantly powerful in that it supports both interactive (i.e. by hand) and fully automated correctness proofs. Failed proof attempts can be used for a more efficient debugging
or verification-based testing. It can be integrated into CASE tools to extract specifications. There have been several extensions to KeY in order to apply it to the verification of C
programs or hybrid systems
. KeY is jointly developed by Karlsruhe Institute of Technology
, Germany; Technische Universität Darmstadt, Germany; and Chalmers University of Technology
in Gothenburg, Sweden and is licensed under the GPL
.
with the resulting changes to program variables stored in so-called updates. Once the program has been processed completely, there remains a first-order logic
proof obligation. At the heart of the KeY system lies a first-order theorem prover based on sequent calculus
, which is used to close the proof. Interference rules are captured in so called taclets which consist of an own simple language to describe changes to a sequent.
called Java Card DL. It is a version of a first-order dynamic logic
tailored to Java Card programs. As such, it for example allows statements (formulas) like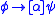 , which intuitively says that the post-condition
, which intuitively says that the post-condition 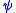 must hold in all program states reachable by executing the Java Card program
must hold in all program states reachable by executing the Java Card program  in any state that satisfies the pre-condition
in any state that satisfies the pre-condition  . This is equivalent to
. This is equivalent to 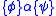 in Hoare calculus if
in Hoare calculus if  and
and  are purely first order. Dynamic logic, however, extends Hoare logic in that formulas may contain nested program modalities such as
are purely first order. Dynamic logic, however, extends Hoare logic in that formulas may contain nested program modalities such as  , or that quantification over formulas which contain modalities is possible. There is also a dual
, or that quantification over formulas which contain modalities is possible. There is also a dual
modality which includes termination
which includes termination
. This dynamic logic can be seen as a special multi-modal logic (with an infinite number of modalities) where for each Java block there are modalities
there are modalities  and
and 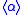 .
.
. A sequent is of the form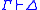 where
where  (assumptions) and
(assumptions) and  (propositions) are sets of formulas with the intuitive meaning that
(propositions) are sets of formulas with the intuitive meaning that  holds true. By means of deduction
holds true. By means of deduction
, an initial sequent representing the proof obligation is shown to be constructible from just fundamental first-order axioms (such as equality ).
).
. For instance, the formula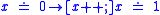 is logically equivalent to
is logically equivalent to  . As this example shows, symbolic execution in dynamic logic is very similar to calculating weakest preconditions. Both
. As this example shows, symbolic execution in dynamic logic is very similar to calculating weakest preconditions. Both 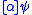 and
and 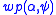 essentially denote the same thing – with two exceptions: Firstly,
essentially denote the same thing – with two exceptions: Firstly,  is a function of some meta-calculus while
is a function of some meta-calculus while 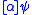 really is a formula of the given calculus. Secondly, symbolic execution runs through the program forward just as an actual execution would. To save intermediate results of assignments, KeY introduces a concept called updates, which are similar to substitutions but are only applied once the program modality has been fully eliminated. Syntactically, updates are consist of parallel (side-effect free) assignments written in curly braces in front of a modality. An example of symbolic execution with updates:
really is a formula of the given calculus. Secondly, symbolic execution runs through the program forward just as an actual execution would. To save intermediate results of assignments, KeY introduces a concept called updates, which are similar to substitutions but are only applied once the program modality has been fully eliminated. Syntactically, updates are consist of parallel (side-effect free) assignments written in curly braces in front of a modality. An example of symbolic execution with updates: 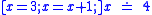 is transformed to
is transformed to 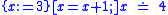 in the first step and to
in the first step and to  in the second step. The modality then is empty and "backwards application" of the update to the postcondition yields a precondition where
in the second step. The modality then is empty and "backwards application" of the update to the postcondition yields a precondition where  could take any value.
could take any value.
 and
and  .
.
int foo (int x, int y) {
int z = 0;
while (y > 0)
if (y % 2 0) {
x = x*2;
y = y/2;
} else {
y = y/2;
z = z+x;
x = x*2;
}
return z;
}
One thus starts the proof with the premise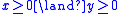 and the to-be-shown conclusion
and the to-be-shown conclusion  . Note that tableaux of sequent calculi are usually written "upside-down", i.e., the starting sequent appears at the bottom and deduction steps go upwards. The proof can be seen in the figure on the right.
. Note that tableaux of sequent calculi are usually written "upside-down", i.e., the starting sequent appears at the bottom and deduction steps go upwards. The proof can be seen in the figure on the right.
of a program as a symbolic execution
tree that contains all feasible execution paths through the program up to a certain point. It is provided as a plugin to the Eclipse
development platform.
tool that can generate unit tests for Java programs. The model from which test data and the test case are derived consists of a formal specification (provided in JML or OCL
) and a symbolic execution tree of the implementation under test which is computed by the KeY system.
Distribution and Variants of the KeY System
KeY is free software written in Java and licensed under GPL. It can be downloaded from the project website in source; currently there are no pre-compiled binaries available. As another possibility, KeY can be executed directly via Java web start
without the need for compilation and installation.
. This calculus can be seen as a subset to the one that is used in the main branch of KeY. Due to the simplicity of the Hoare calculus, this implementation is essentially meant to exemplify formal methods in undergraduate classes.
It extends the KeY tool with computer algebra systems like Mathematica
and corresponding algorithms and proof strategies such that it can be used for practical verification of hybrid systems.
KeYmaera has been developed at the University of Oldenburg and the Carnegie Mellon University
. The name of the tool was chosen as a homophone
to Chimera
, the hybrid animal from ancient Greek mythology.
, a subset of the C programming language. This variant is no longer supported.
. This variant is no longer supported; more information can be found on the weblink below.
Sources
External links
Formal verification
In the context of hardware and software systems, formal verification is the act of proving or disproving the correctness of intended algorithms underlying a system with respect to a certain formal specification or property, using formal methods of mathematics .- Usage :Formal verification can be...
of Java
Java (programming language)
Java is a programming language originally developed by James Gosling at Sun Microsystems and released in 1995 as a core component of Sun Microsystems' Java platform. The language derives much of its syntax from C and C++ but has a simpler object model and fewer low-level facilities...
programs.It accepts both specifications written in JML
Java Modeling Language
The Java Modeling Language is a specification language for Java programs, using Hoare style pre- and postconditions and invariants, that follows the design by contract paradigm...
or OCL
Object Constraint Language
The Object Constraint Language is a declarative language for describing rules that apply to Unified Modeling Language models developed at IBM and now part of the UML standard. Initially, OCL was only a formal specification language extension to UML. OCL may now be used with any Meta-Object...
to Java source files. These are transformed into theorems of dynamic logic
Dynamic logic
Dynamic logic may mean:* In theoretical computer science, dynamic logic is a modal logic for reasoning about dynamic behaviour* In digital electronics, dynamic logic is a technique used for combinatorial circuit design* A different concept proposed by Leonid Perlovsky...
and then compared against program semantics which are likewise defined in terms of dynamic logic. KeY is significantly powerful in that it supports both interactive (i.e. by hand) and fully automated correctness proofs. Failed proof attempts can be used for a more efficient debugging
Debugging
Debugging is a methodical process of finding and reducing the number of bugs, or defects, in a computer program or a piece of electronic hardware, thus making it behave as expected. Debugging tends to be harder when various subsystems are tightly coupled, as changes in one may cause bugs to emerge...
or verification-based testing. It can be integrated into CASE tools to extract specifications. There have been several extensions to KeY in order to apply it to the verification of C
C (programming language)
C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....
programs or hybrid systems
Hybrid system
A hybrid system is a dynamic system that exhibits both continuous and discrete dynamic behavior – a system that can both flow and jump...
. KeY is jointly developed by Karlsruhe Institute of Technology
Karlsruhe Institute of Technology
The Karlsruhe Institute of Technology is a German academic research and education institution with university status resulting from a merger of the university and the research center of the city of Karlsruhe. The university, also known as Fridericiana, was founded in 1825...
, Germany; Technische Universität Darmstadt, Germany; and Chalmers University of Technology
Chalmers University of Technology
Chalmers University of Technology , is a Swedish university located in Gothenburg that focuses on research and education in technology, natural science and architecture.-History:...
in Gothenburg, Sweden and is licensed under the GPL
GNU General Public License
The GNU General Public License is the most widely used free software license, originally written by Richard Stallman for the GNU Project....
.
Overview
The usual user input to KeY consists of a Java source file with annotations in either JML or OCL. Both, they are translated to KeY's internal represenation, dynamic logic. From the given specifications, several proof obligations arise which are to be discharged, i.e. a proof has to be found. To this ends, the program is symbolically executedSymbolic execution
In computer science, symbolic execution refers to the analysis of programs by tracking symbolic rather than actual values, a case of abstract interpretation. The field of symbolic simulation applies the same concept to hardware...
with the resulting changes to program variables stored in so-called updates. Once the program has been processed completely, there remains a first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
proof obligation. At the heart of the KeY system lies a first-order theorem prover based on sequent calculus
Sequent calculus
In proof theory and mathematical logic, sequent calculus is a family of formal systems sharing a certain style of inference and certain formal properties. The first sequent calculi, systems LK and LJ, were introduced by Gerhard Gentzen in 1934 as a tool for studying natural deduction in...
, which is used to close the proof. Interference rules are captured in so called taclets which consist of an own simple language to describe changes to a sequent.
Java Card DL
The theoretical foundation of KeY is a formal logicFormal logic
Classical or traditional system of determining the validity or invalidity of a conclusion deduced from two or more statements...
called Java Card DL. It is a version of a first-order dynamic logic
Dynamic logic (modal logic)
Dynamic logic is an extension of modal logic originally intended for reasoning about computer programs and later applied to more general complex behaviors arising in linguistics, philosophy, AI, and other fields.-Language:...
tailored to Java Card programs. As such, it for example allows statements (formulas) like
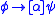 , which intuitively says that the post-condition
, which intuitively says that the post-condition 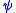 must hold in all program states reachable by executing the Java Card program
must hold in all program states reachable by executing the Java Card program  in any state that satisfies the pre-condition
in any state that satisfies the pre-condition  . This is equivalent to
. This is equivalent to 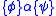 in Hoare calculus if
in Hoare calculus if  and
and  are purely first order. Dynamic logic, however, extends Hoare logic in that formulas may contain nested program modalities such as
are purely first order. Dynamic logic, however, extends Hoare logic in that formulas may contain nested program modalities such as  , or that quantification over formulas which contain modalities is possible. There is also a dual
, or that quantification over formulas which contain modalities is possible. There is also a dualDuality (mathematics)
In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
modality
 which includes termination
which includes terminationTermination analysis
In computer science, a termination analysis is program analysis which attempts to determine whether the evaluation of a given program will definitely terminate. Because the halting problem is undecidable, termination analysis cannot work correctly in all cases. The aim is to find the answer...
. This dynamic logic can be seen as a special multi-modal logic (with an infinite number of modalities) where for each Java block
 there are modalities
there are modalities  and
and 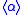 .
.Deduction component
At the heart of the KeY system lies a first-order theorem prover based on a sequent calculusSequent calculus
In proof theory and mathematical logic, sequent calculus is a family of formal systems sharing a certain style of inference and certain formal properties. The first sequent calculi, systems LK and LJ, were introduced by Gerhard Gentzen in 1934 as a tool for studying natural deduction in...
. A sequent is of the form
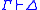 where
where  (assumptions) and
(assumptions) and  (propositions) are sets of formulas with the intuitive meaning that
(propositions) are sets of formulas with the intuitive meaning that  holds true. By means of deduction
holds true. By means of deductionDeductive reasoning
Deductive reasoning, also called deductive logic, is reasoning which constructs or evaluates deductive arguments. Deductive arguments are attempts to show that a conclusion necessarily follows from a set of premises or hypothesis...
, an initial sequent representing the proof obligation is shown to be constructible from just fundamental first-order axioms (such as equality
 ).
).Symbolic execution of Java code
During that, program modalities are eliminated by symbolic executionSymbolic execution
In computer science, symbolic execution refers to the analysis of programs by tracking symbolic rather than actual values, a case of abstract interpretation. The field of symbolic simulation applies the same concept to hardware...
. For instance, the formula
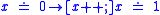 is logically equivalent to
is logically equivalent to  . As this example shows, symbolic execution in dynamic logic is very similar to calculating weakest preconditions. Both
. As this example shows, symbolic execution in dynamic logic is very similar to calculating weakest preconditions. Both 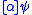 and
and 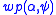 essentially denote the same thing – with two exceptions: Firstly,
essentially denote the same thing – with two exceptions: Firstly,  is a function of some meta-calculus while
is a function of some meta-calculus while 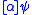 really is a formula of the given calculus. Secondly, symbolic execution runs through the program forward just as an actual execution would. To save intermediate results of assignments, KeY introduces a concept called updates, which are similar to substitutions but are only applied once the program modality has been fully eliminated. Syntactically, updates are consist of parallel (side-effect free) assignments written in curly braces in front of a modality. An example of symbolic execution with updates:
really is a formula of the given calculus. Secondly, symbolic execution runs through the program forward just as an actual execution would. To save intermediate results of assignments, KeY introduces a concept called updates, which are similar to substitutions but are only applied once the program modality has been fully eliminated. Syntactically, updates are consist of parallel (side-effect free) assignments written in curly braces in front of a modality. An example of symbolic execution with updates: 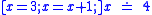 is transformed to
is transformed to 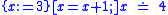 in the first step and to
in the first step and to  in the second step. The modality then is empty and "backwards application" of the update to the postcondition yields a precondition where
in the second step. The modality then is empty and "backwards application" of the update to the postcondition yields a precondition where  could take any value.
could take any value.Example
Suppose one wants to prove that the following method calculates the product of some non-negative integers and
and  .
.int foo (int x, int y) {
int z = 0;
while (y > 0)
if (y % 2 0) {
x = x*2;
y = y/2;
} else {
y = y/2;
z = z+x;
x = x*2;
}
return z;
}
One thus starts the proof with the premise
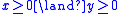 and the to-be-shown conclusion
and the to-be-shown conclusion  . Note that tableaux of sequent calculi are usually written "upside-down", i.e., the starting sequent appears at the bottom and deduction steps go upwards. The proof can be seen in the figure on the right.
. Note that tableaux of sequent calculi are usually written "upside-down", i.e., the starting sequent appears at the bottom and deduction steps go upwards. The proof can be seen in the figure on the right.Symbolic Execution Debugger
The Symbolic Execution Debugger visualizes the control flowControl flow
In computer science, control flow refers to the order in which the individual statements, instructions, or function calls of an imperative or a declarative program are executed or evaluated....
of a program as a symbolic execution
Symbolic execution
In computer science, symbolic execution refers to the analysis of programs by tracking symbolic rather than actual values, a case of abstract interpretation. The field of symbolic simulation applies the same concept to hardware...
tree that contains all feasible execution paths through the program up to a certain point. It is provided as a plugin to the Eclipse
Eclipse (software)
Eclipse is a multi-language software development environment comprising an integrated development environment and an extensible plug-in system...
development platform.
Test Case Generator
KeY is usable as a model-based testingModel-based testing
Model-based testing is the application of Model based design for designing and optionally executing the necessary artifacts to perform software testing. Models can be used to represent the desired behavior of the System Under Test , or to represent the desired testing strategies and testing...
tool that can generate unit tests for Java programs. The model from which test data and the test case are derived consists of a formal specification (provided in JML or OCL
Object Constraint Language
The Object Constraint Language is a declarative language for describing rules that apply to Unified Modeling Language models developed at IBM and now part of the UML standard. Initially, OCL was only a formal specification language extension to UML. OCL may now be used with any Meta-Object...
) and a symbolic execution tree of the implementation under test which is computed by the KeY system.
Distribution and Variants of the KeY System
KeY is free software written in Java and licensed under GPL. It can be downloaded from the project website in source; currently there are no pre-compiled binaries available. As another possibility, KeY can be executed directly via Java web start
Java Web Start
In computing, Java Web Start is a framework developed by Sun Microsystems that allows users to start application software for the Java Platform directly from the Internet using a web browser....
without the need for compilation and installation.
KeY-Hoare
KeY-Hoare is built on top of KeY and features a Hoare calculus with state updates. State updates are a means of describing state transitions in a Kripke structureKripke structure
A Kripke structure is a type of nondeterministic finite state machine proposed by Saul Kripke , used in model checking to represent the behavior of a system.It is a simple abstract machine to capture an idea of a computing machine,...
. This calculus can be seen as a subset to the one that is used in the main branch of KeY. Due to the simplicity of the Hoare calculus, this implementation is essentially meant to exemplify formal methods in undergraduate classes.
KeYmaera
KeYmaera http://symbolaris.com/info/KeYmaera.html (previously called HyKeY) is a deductive verification tool for hybrid systems based on a calculus for the differential dynamic logic dL http://symbolaris.com/logic/dL.html.It extends the KeY tool with computer algebra systems like Mathematica
Mathematica
Mathematica is a computational software program used in scientific, engineering, and mathematical fields and other areas of technical computing...
and corresponding algorithms and proof strategies such that it can be used for practical verification of hybrid systems.
KeYmaera has been developed at the University of Oldenburg and the Carnegie Mellon University
Carnegie Mellon University
Carnegie Mellon University is a private research university in Pittsburgh, Pennsylvania, United States....
. The name of the tool was chosen as a homophone
Homophone
A homophone is a word that is pronounced the same as another word but differs in meaning. The words may be spelled the same, such as rose and rose , or differently, such as carat, caret, and carrot, or to, two, and too. Homophones that are spelled the same are also both homographs and homonyms...
to Chimera
Chimera (mythology)
The Chimera or Chimaera was, according to Greek mythology, a monstrous fire-breathing female creature of Lycia in Asia Minor, composed of the parts of multiple animals: upon the body of a lioness with a tail that ended in a snake's head, the head of a goat arose on her back at the center of her...
, the hybrid animal from ancient Greek mythology.
KeY for C
KeY for C is an adaption of the KeY System to MISRA CMISRA C
MISRA C is a software development standard for the C programming language developed by MISRA . Its aims are to facilitate code safety, portability and reliability in the context of embedded systems, specifically those systems programmed in ISO C...
, a subset of the C programming language. This variant is no longer supported.
ASMKeY
There is also an adaptation to use KeY for the symbolic execution of Abstract State Machines, that was developed at ETH ZürichETH Zurich
The Swiss Federal Institute of Technology Zurich or ETH Zürich is an engineering, science, technology, mathematics and management university in the City of Zurich, Switzerland....
. This variant is no longer supported; more information can be found on the weblink below.
Sources
- Verification of Object-Oriented Software: The KeY Approach. Bernhard Beckert, Reiner Hähnle, Peter H. Schmitt (Eds.). SpringerSpringer Science+Business Media- Selected publications :* Encyclopaedia of Mathematics* Ergebnisse der Mathematik und ihrer Grenzgebiete * Graduate Texts in Mathematics * Grothendieck's Séminaire de géométrie algébrique...
, 2007. ISBN 978-3-540-68977-5. - A comparison of tools for teaching formal software verification. Ingo Feinerer and Gernot Salzer. SpringerSpringer Science+Business Media- Selected publications :* Encyclopaedia of Mathematics* Ergebnisse der Mathematik und ihrer Grenzgebiete * Graduate Texts in Mathematics * Grothendieck's Séminaire de géométrie algébrique...
, 2008 - Programming With Proofs: Language Based Approaches To Totally Correct Software. Aaron Stump. Verified Software: Theories, Tools, and Experiments, 2005.
- High Assurance (for Security or Safety) and Free-Libre / Open Source Software (FLOSS). David Wheeler, 2009
External links

