
Keccak
Encyclopedia
Keccak is a cryptographic hash function
designed by Guido Bertoni, Joan Daemen
, Michaël Peeters and Gilles Van Assche. Keccak is one of five finalists in the NIST hash function competition
to select a SHA-3 algorithm. The authors claim 12.5 cycles per byte
on an Intel Core 2 CPU. It is notably faster than all other finalists in hardware implementations.
Keccak uses the sponge construction in which message blocks are XORed into the initial bits of the state, which is then invertibly permuted. In its largest instance, the state consists of a 5×5 array of 64-bit words, 1600 bits total. Reduced versions of the algorithm are defined for smaller power-of-2 word sizes w down to 1 bit (25 bits total state). While smaller state sizes can be used to test cryptanalytic attacks, intermediate state sizes (e.g., from w=4, 100 bits, to w=32, 800 bits) also provide practical, lightweight, alternatives.
The state can be considered to be a 5×5×w array of bits. Let a[i][j][k] be bit (i×5 + j)×w + k of the input, using a little-endian convention. All index arithmetic is performed modulo 5 or w.
The basic block permutation function consists of 12+2ℓ iterations of five sub-rounds, each individually very simple:
θ
ρ
π
χ
ι
To absorb r bits of data, the data is XORed into the leading bits of the state, and the block permutation is applied. To squeeze, the first r bits of the state are produced as output, and the block permutation is applied if additional output is desired.
Central to this is the "capacity" of the hash function, which is the c=1600−r state bits that are not touched by input or output. This can be adjusted based on security requirements, but Keccak's SHA-3 proposal sets a conservative c=2n, where n is the size of the output hash. Thus r, the number of message bits processed per block permutation, depends on the output hash size. It is 1152, 1088, 832, or 576 (144, 136, 104 and 72 bytes) for 224, 256, 384 and 512-bit hash sizes, respectively.
To ensure the message can be evenly divided into r-bit blocks, it is padded with the bit pattern 10*1: a 1 bit, zero or more 0 bits (maximum r−1), and a final 1 bit. The final 1 bit is required because the sponge construction security proof requires that the final message block is not all-zero.
To compute a Keccak hash, initialize the state to 0, pad the input, and break it into r-bit pieces. Absorb the input into the state; that is, for each piece, XOR it into the state and then apply the block permutation.
After the final block permutation, the leading n bits of the state are the desired hash. Because r is always greater than n, there is actually never a need for additional block permutations in the squeezing phase. However, arbitrary output length may be useful in applications such as optimal asymmetric encryption padding
. In this case, n is a security parameter rather than the output size.
Although not part of the SHA-3 competition requirements, smaller variants of the block permutation can be used, for hash output sizes up to half their state size, if the rate r is limited appropriately. For example, a 256-bit hash can be computed using 25 32-bit words if r = 800−2×256 = 288 (36 bytes per iteration).
Cryptographic hash function
A cryptographic hash function is a deterministic procedure that takes an arbitrary block of data and returns a fixed-size bit string, the hash value, such that an accidental or intentional change to the data will change the hash value...
designed by Guido Bertoni, Joan Daemen
Joan Daemen
Joan Daemen |Limburg]], Belgium) is a Belgian cryptographer and one of the designers of Rijndael, the Advanced Encryption Standard , together with Vincent Rijmen. He has also designed or co-designed the MMB, Square, SHARK, NOEKEON, 3-Way, and BaseKing block ciphers...
, Michaël Peeters and Gilles Van Assche. Keccak is one of five finalists in the NIST hash function competition
NIST hash function competition
The NIST hash function competition is an open competition held by the US National Institute of Standards and Technology for a new SHA-3 function to replace the older SHA-1 and SHA-2, which was formally announced in the Federal Register on November 2, 2007...
to select a SHA-3 algorithm. The authors claim 12.5 cycles per byte
Cycles per byte
Cycles per byte is a unit of measurement which indicates the number of clock cycles a microprocessor will perform per byte of data processed in an algorithm. It is commonly used as a partial indicator of real-world performance in cryptographic functions....
on an Intel Core 2 CPU. It is notably faster than all other finalists in hardware implementations.
Keccak uses the sponge construction in which message blocks are XORed into the initial bits of the state, which is then invertibly permuted. In its largest instance, the state consists of a 5×5 array of 64-bit words, 1600 bits total. Reduced versions of the algorithm are defined for smaller power-of-2 word sizes w down to 1 bit (25 bits total state). While smaller state sizes can be used to test cryptanalytic attacks, intermediate state sizes (e.g., from w=4, 100 bits, to w=32, 800 bits) also provide practical, lightweight, alternatives.
The Keccak block permutation
This is defined for any power of two word size, w = 2ℓ bits. The main SHA-3 submission uses 64-bit words, ℓ = 6.The state can be considered to be a 5×5×w array of bits. Let a[i][j][k] be bit (i×5 + j)×w + k of the input, using a little-endian convention. All index arithmetic is performed modulo 5 or w.
The basic block permutation function consists of 12+2ℓ iterations of five sub-rounds, each individually very simple:
θ
- Compute the parity of each of the 320 5-bit columns, and exclusive-or that into two nearby columns in a regular pattern. To be precise, a[i][j][k] ⊕= parity(a[0..4][j−1][k]) ⊕ parity(a[0..4][j+1][k−1])
ρ
- Bitwise rotate each of the 25 words by a different triangular number 0, 1, 3, 6, 10, 15, …. To be precise, a[0][0] is not rotated, and for all 0≤t≤24, a[i][j][k] = a[i][j][k−(t+1)(t+2)/2], where
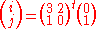 .
.
π
- Permute the 25 words in a fixed pattern. a[3i+2j][i] = a[i][j]
χ
- Bitwise combine along rows, using a = a ⊕ (¬b & c). To be precise, a[i][j][k] ⊕= ¬a[i][j+1][k] & a[i][j+2][k]. This is the only non-linear operation in Keccak.
ι
- Exclusive-or a round constant into one word of the state. To be precise, in round n, for 0≤m≤ℓ, a[0][0][2m−1] is exclusive-ORed with bit m+7n of a degree-8 LFSR sequence. This breaks the symmetry that is preserved by the other sub-rounds.
Hashing variable-length messages
Keccak uses the "sponge construction", where input is "absorbed" into the hash state at a given rate, then an output hash is "squeezed" from it at the same rate.To absorb r bits of data, the data is XORed into the leading bits of the state, and the block permutation is applied. To squeeze, the first r bits of the state are produced as output, and the block permutation is applied if additional output is desired.
Central to this is the "capacity" of the hash function, which is the c=1600−r state bits that are not touched by input or output. This can be adjusted based on security requirements, but Keccak's SHA-3 proposal sets a conservative c=2n, where n is the size of the output hash. Thus r, the number of message bits processed per block permutation, depends on the output hash size. It is 1152, 1088, 832, or 576 (144, 136, 104 and 72 bytes) for 224, 256, 384 and 512-bit hash sizes, respectively.
To ensure the message can be evenly divided into r-bit blocks, it is padded with the bit pattern 10*1: a 1 bit, zero or more 0 bits (maximum r−1), and a final 1 bit. The final 1 bit is required because the sponge construction security proof requires that the final message block is not all-zero.
To compute a Keccak hash, initialize the state to 0, pad the input, and break it into r-bit pieces. Absorb the input into the state; that is, for each piece, XOR it into the state and then apply the block permutation.
After the final block permutation, the leading n bits of the state are the desired hash. Because r is always greater than n, there is actually never a need for additional block permutations in the squeezing phase. However, arbitrary output length may be useful in applications such as optimal asymmetric encryption padding
Optimal Asymmetric Encryption Padding
In cryptography, Optimal Asymmetric Encryption Padding is a padding scheme often used together with RSA encryption. OAEP was introduced by Bellare and Rogaway....
. In this case, n is a security parameter rather than the output size.
Although not part of the SHA-3 competition requirements, smaller variants of the block permutation can be used, for hash output sizes up to half their state size, if the rate r is limited appropriately. For example, a 256-bit hash can be computed using 25 32-bit words if r = 800−2×256 = 288 (36 bytes per iteration).
Tweaks
Throughout the NIST hash function competition, entrants are permitted to "tweak" their algorithms to address issues that are discovered. Changes that have been made to Keccak are:- The number of rounds was increased from 12+ℓ to 12+2ℓ to be more conservative about security.
- The message padding was changed from a more complex scheme to the simple 10*1 pattern described above.
- The rate r was increased to the security limit, rather than rounding down to the nearest power of 2.

