In mathematics, Kemnitz's conjecture states that the centroid

Centroid

In geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...

 of a certain set of lattice points in plane is also a lattice point. It was proved independently in the autumn of 2003 by Christian Reiher

Christian Reiher

Christian Reiher is a German mathematician. He is the second most successful participant in the history of the International Mathematical Olympiad, having won four gold medals in the years 2000 to 2003 and a bronze medal in 1999.Just after finishing his Abitur, he proved Kemnitz's conjecture, an...

 and Carlos di Fiore.

The exact formulation of this conjecture is as follows:

Let be a natural number and a set of 4n − 3 lattice points in plane. Then there exists a subset 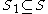with points such that the centroid of all points from is also a lattice point.

The Kemnitz's conjecture was formulated in 1983 by Arnfried Kemnitz as a generalization of the Erdős–Ginzburg–Ziv theorem

Zero-sum problem

In number theory, zero-sum problems are a certain class of combinatorial questions. In general, a finite abelian group G is considered. The zero-sum problem for the integer n is the following: Find the smallest integer k such that every sequence of elements of G with length k contains n terms that...

. In 2000, Lajos Rónyai proved the conjecture for sets with 4n − 2 lattice points. Then, in 2003, Christian Reiher proved the full conjecture using the Chevalley–Warning theorem.