Zero-sum problem
Encyclopedia
In number theory
, zero-sum problems are a certain class of combinatorial questions. In general, a finite abelian group G is considered. The zero-sum problem for the integer n is the following: Find the smallest integer k such that every sequence of elements of G with length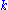
contains n terms that sum to 0
.
In 1961 Paul Erdős
, Abraham Ginzburg, and Abraham Ziv proved the general result for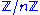
(the integers mod
n) that
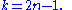
Explicitly this says that any multiset
of 2n − 1 integers has a subset of size n the sum of whose elements is a multiple of n. This result is generally known as the EGZ theorem after its discoverers.
More general results than this theorem exist, such as Olson's theorem, Kemnitz's conjecture
(proved by Christian Reiher
in 2003), and the weighted EGZ theorem (proved by David J. Grynkiewicz in 2005).
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, zero-sum problems are a certain class of combinatorial questions. In general, a finite abelian group G is considered. The zero-sum problem for the integer n is the following: Find the smallest integer k such that every sequence of elements of G with length
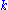contains n terms that sum to 0Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
.
In 1961 Paul Erdős
Paul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
, Abraham Ginzburg, and Abraham Ziv proved the general result for
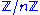(the integers modModular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
n) that
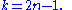
Explicitly this says that any multiset
Multiset
In mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...
of 2n − 1 integers has a subset of size n the sum of whose elements is a multiple of n. This result is generally known as the EGZ theorem after its discoverers.
More general results than this theorem exist, such as Olson's theorem, Kemnitz's conjecture
Kemnitz's conjecture
In mathematics, Kemnitz's conjecture states that the centroid of a certain set of lattice points in plane is also a lattice point. It was proved independently in the autumn of 2003 by Christian Reiher and Carlos di Fiore....
(proved by Christian Reiher
Christian Reiher
Christian Reiher is a German mathematician. He is the second most successful participant in the history of the International Mathematical Olympiad, having won four gold medals in the years 2000 to 2003 and a bronze medal in 1999.Just after finishing his Abitur, he proved Kemnitz's conjecture, an...
in 2003), and the weighted EGZ theorem (proved by David J. Grynkiewicz in 2005).
External links
- PlanetMath Erdős, Ginzburg, Ziv Theorem
- Sun, Zhi-WeiZhi-Wei SunZhi-Wei Sun is a Chinese mathematician, working primarily on number theory, combinatorics, and group theory. Currently he works as a professor in Nanjing University....
, "Covering Systems, Restricted Sumsets, Zero-sum Problems and their Unification"