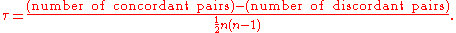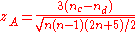Kendall tau rank correlation coefficient
Encyclopedia
In statistics
, the Kendall rank correlation coefficient, commonly referred to as Kendall's tau (τ) coefficient, is a statistic
used to measure the association
between two measured quantities. A tau test is a non-parametric
hypothesis test which uses the coefficient to test for statistical dependence.
Specifically, it is a measure of rank correlation
: that is, the similarity of the orderings of the data when ranked by each of the quantities. It is named after Maurice Kendall
, who developed it in 1938, though Gustav Fechner
had proposed a similar measure in the context of time series
in 1897.
The Kendall τ coefficient is defined as:
in a statistical hypothesis test
to establish whether two variables may be regarded as statistically dependent. This test is non-parametric
, as it does not rely on any assumptions on the distributions of X or Y.
Under a null hypothesis
of X and Y being independent, the sampling distribution
of τ will have an expected value
of zero. The precise distribution cannot be characterized in terms of common distributions, but may be calculated exactly for small samples; for larger samples, it is common to use an approximation to the normal distribution, with mean zero and variance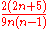
.
s. Both variables have to be ordinal. Tau-a will not make any adjustment for ties.
The Kendall tau-b coefficient is defined as:
where
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the Kendall rank correlation coefficient, commonly referred to as Kendall's tau (τ) coefficient, is a statistic
Statistic
A statistic is a single measure of some attribute of a sample . It is calculated by applying a function to the values of the items comprising the sample which are known together as a set of data.More formally, statistical theory defines a statistic as a function of a sample where the function...
used to measure the association
Association (statistics)
In statistics, an association is any relationship between two measured quantities that renders them statistically dependent. The term "association" refers broadly to any such relationship, whereas the narrower term "correlation" refers to a linear relationship between two quantities.There are many...
between two measured quantities. A tau test is a non-parametric
Non-parametric statistics
In statistics, the term non-parametric statistics has at least two different meanings:The first meaning of non-parametric covers techniques that do not rely on data belonging to any particular distribution. These include, among others:...
hypothesis test which uses the coefficient to test for statistical dependence.
Specifically, it is a measure of rank correlation
Rank correlation
In statistics, a rank correlation is the relationship between different rankings of the same set of items. A rank correlation coefficient measures the degree of similarity between two rankings, and can be used to assess its significance....
: that is, the similarity of the orderings of the data when ranked by each of the quantities. It is named after Maurice Kendall
Maurice Kendall
Sir Maurice George Kendall, FBA was a British statistician, widely known for his contribution to statistics. The Kendall tau rank correlation is named after him.-Education and early life:...
, who developed it in 1938, though Gustav Fechner
Gustav Fechner
Gustav Theodor Fechner , was a German experimental psychologist. An early pioneer in experimental psychology and founder of psychophysics, he inspired many 20th century scientists and philosophers...
had proposed a similar measure in the context of time series
Time series
In statistics, signal processing, econometrics and mathematical finance, a time series is a sequence of data points, measured typically at successive times spaced at uniform time intervals. Examples of time series are the daily closing value of the Dow Jones index or the annual flow volume of the...
in 1897.
Definition
Let (x1, y1), (x2, y2), …, (xn, yn) be a set of joint observations from two random variables X and Y respectively, such that all the values of (xi) and (yi) are unique. Any pair of observations (xi, yi) and (xj, yj) are said to be concordant if the ranks for both elements agree: that is, if both xi > xj and yi > yj or if both xi < xj and yi < yj. They are said to be discordant, if xi > xj and yi < yj or if xi < xj and yi > yj. If xi = xj or yi = yj, the pair is neither concordant nor discordant.The Kendall τ coefficient is defined as:
Properties
The denominator is the total number of pairs, so the coefficient must be in the range −1 ≤ τ ≤ 1.- If the agreement between the two rankings is perfect (i.e., the two rankings are the same) the coefficient has value 1.
- If the disagreement between the two rankings is perfect (i.e., one ranking is the reverse of the other) the coefficient has value −1.
- If X and Y are independent, then we would expect the coefficient to be approximately zero.
Hypothesis test
The Kendall rank coefficient is often used as a test statisticTest statistic
In statistical hypothesis testing, a hypothesis test is typically specified in terms of a test statistic, which is a function of the sample; it is considered as a numerical summary of a set of data that...
in a statistical hypothesis test
Statistical hypothesis testing
A statistical hypothesis test is a method of making decisions using data, whether from a controlled experiment or an observational study . In statistics, a result is called statistically significant if it is unlikely to have occurred by chance alone, according to a pre-determined threshold...
to establish whether two variables may be regarded as statistically dependent. This test is non-parametric
Non-parametric statistics
In statistics, the term non-parametric statistics has at least two different meanings:The first meaning of non-parametric covers techniques that do not rely on data belonging to any particular distribution. These include, among others:...
, as it does not rely on any assumptions on the distributions of X or Y.
Under a null hypothesis
Null hypothesis
The practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
of X and Y being independent, the sampling distribution
Sampling distribution
In statistics, a sampling distribution or finite-sample distribution is the probability distribution of a given statistic based on a random sample. Sampling distributions are important in statistics because they provide a major simplification on the route to statistical inference...
of τ will have an expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of zero. The precise distribution cannot be characterized in terms of common distributions, but may be calculated exactly for small samples; for larger samples, it is common to use an approximation to the normal distribution, with mean zero and variance
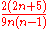.Accounting for ties
A pair {(xi, yi), (xj, yj)} is said to be tied if xi = xj or yi = yj; a tied pair is neither concordant nor discordant. When tied pairs arise in the data, the coefficient may be modified in a number of ways to keep it in the range [-1, 1]:Tau-a
Tau-a statistic tests the strength of association of the cross tabulationCross tabulation
Cross tabulation is the process of creating a contingency table from the multivariate frequency distribution of statistical variables. Heavily used in survey research, cross tabulations can be produced by a range of statistical packages, including some that are specialised for the task. Survey...
s. Both variables have to be ordinal. Tau-a will not make any adjustment for ties.
Tau-b
Tau-b statistic, unlike tau-a, makes adjustments for ties and is suitable for square tables. Values of tau-b range from −1 (100% negative association, or perfect inversion) to +1 (100% positive association, or perfect agreement). A value of zero indicates the absence of association.The Kendall tau-b coefficient is defined as:
where
-
Tau-c
Tau-c differs from tau-b as in being more suitable for rectangular tables than for square tables.
Significance tests
When two quantities are statistically independent, the distribution of
is not easily characterizable in terms of known distributions. However, for 
the following statistic, 
, is approximately characterized by a standard normal distribution when the quantities are statistically independent:
Thus, if you want to test whether two quantities are statistically dependent, compute
, and find the cumulative probability for a standard normal distribution at 
. For a 2-tailed test, multiply that number by two and this gives you the p-value. If the p-value is below your acceptance level (typically 5%), you can reject the null hypothesis that the quantities are statistically independent and accept the hypothesis that they are dependent.
Numerous adjustments should be added to
when accounting for ties. The following statistic, 
, provides an approximation coinciding with the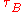 
distribution and is again approximately characterized by a standard normal distribution when the quantities are statistically independent:
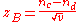
where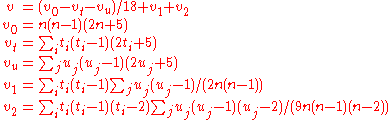
Algorithms
The direct computation of the numerator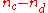
, involves two nested iterations, as characterized by the following pseudo-code:
numer := 0
for i:=1..N do
for j:=1..(i-1) do
numer := numer + sgn(x[i] - x[j]) * sgn(y[i] - y[j])
return numer
Although quick to implement, this algorithm is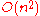
in complexity and becomes very slow on large samples. A more sophisticated algorithm built upon the Merge SortMerge sortMerge sort is an O comparison-based sorting algorithm. Most implementations produce a stable sort, meaning that the implementation preserves the input order of equal elements in the sorted output. It is a divide and conquer algorithm...
algorithm can be used to compute the numerator in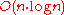
time.
Begin by ordering your data points sorting by the first quantity,
, and secondarily (among ties in 
) by the second quantity, 
. With this initial ordering,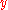 
is not sorted, and the core of the algorithm consists of computing how many steps a Bubble SortBubble sortBubble sort, also known as sinking sort, is a simple sorting algorithm that works by repeatedly stepping through the list to be sorted, comparing each pair of adjacent items and swapping them if they are in the wrong order. The pass through the list is repeated until no swaps are needed, which...
would take to sort this initial
. An enhanced Merge SortMerge sortMerge sort is an O comparison-based sorting algorithm. Most implementations produce a stable sort, meaning that the implementation preserves the input order of equal elements in the sorted output. It is a divide and conquer algorithm...
algorithm, with
complexity, can be applied to compute the number of swaps,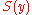 
, that would be required by a Bubble SortBubble sortBubble sort, also known as sinking sort, is a simple sorting algorithm that works by repeatedly stepping through the list to be sorted, comparing each pair of adjacent items and swapping them if they are in the wrong order. The pass through the list is repeated until no swaps are needed, which...
to sort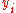
. Then the numerator for 
is computed as:
,
where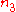
is computed like 
and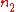 
, but with respect to the joint ties in 
and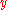 
.
A Merge SortMerge sortMerge sort is an O comparison-based sorting algorithm. Most implementations produce a stable sort, meaning that the implementation preserves the input order of equal elements in the sorted output. It is a divide and conquer algorithm...
partitions the data to be sorted,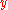
into two roughly equal halves, 
and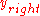 
, then sorts each half recursive, and then merges the two sorted halves into a fully sorted vector. The number of Bubble SortBubble sortBubble sort, also known as sinking sort, is a simple sorting algorithm that works by repeatedly stepping through the list to be sorted, comparing each pair of adjacent items and swapping them if they are in the wrong order. The pass through the list is repeated until no swaps are needed, which...
swaps is equal to:
where
and 
are the sorted versions of 
and 
, and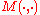 
characterizes the Bubble SortBubble sortBubble sort, also known as sinking sort, is a simple sorting algorithm that works by repeatedly stepping through the list to be sorted, comparing each pair of adjacent items and swapping them if they are in the wrong order. The pass through the list is repeated until no swaps are needed, which...
swap-equivalent for a merge operation.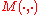
is computed as depicted in the following pseudo-code:
function M(L[1..n], R[1..m])
n := n + m
i := 1
j := 1
nSwaps := 0
while i + j <= n do
if i > m or R[j] < L[i] then
nSwaps := nSwaps + m - (i-1)
j := j + 1
else
i := i + 1
return nSwaps
A side effect of the above steps is that you end up with both a sorted version of
and a sorted version of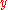 
. With these, the factors 
and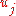 
used to compute 
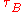are easily obtained in a single linear-time pass through the sorted arrays.
A second algorithm with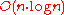
time complexity, based on AVT trees, was devised by David Christensen.
See also
- CorrelationCorrelationIn statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
- Kendall tau distanceKendall tau distanceThe Kendall tau distance is a metric that counts the number of pairwise disagreements between two lists. The larger the distance, the more dissimilar the two lists are. Kendall tau distance is also called bubble-sort distance since it is equivalent to the number of swaps that the bubble sort...
- Kendall's WKendall's WKendall's W is a non-parametric statistic. It is a normalization of the statistic of the Friedman test, and can be used for assessing agreement among raters...
- Spearman's rank correlation coefficientSpearman's rank correlation coefficientIn statistics, Spearman's rank correlation coefficient or Spearman's rho, named after Charles Spearman and often denoted by the Greek letter \rho or as r_s, is a non-parametric measure of statistical dependence between two variables. It assesses how well the relationship between two variables can...
- Gamma test (statistics)Gamma test (statistics)In statistics, a gamma test tests the strength of association of the cross tabulated data when both variables are measured at the ordinal level. It makes no adjustment for either table size or ties. Values range from −1 to +1...
- Theil–Sen estimatorTheil–Sen estimatorIn non-parametric statistics, the Theil–Sen estimator, also known as Sen's slope estimator, slope selection, the single median method, or the Kendall robust line-fit method, is a method for robust linear regression that chooses the median slope among all lines through pairs of two-dimensional...
External links
-
