Khintchine inequality
Encyclopedia
In mathematics
, the Khintchine inequality, named after Aleksandr Khinchin and spelled in multiple ways in the Roman alphabet, is a theorem from probability
, and is also frequently used in analysis
. Heuristically, it says that if we pick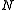
complex numbers 
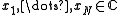, and add them together each multiplied by a random sign 
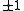, then the expected value
of its modulus
, or the modulus it will be closest to on average, will be not too far off from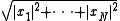
.
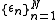be i.i.d. random variables
with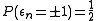
for every 
,
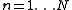i.e., a sequence with Rademacher distribution.
Let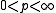
and let 
.
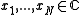Then
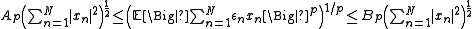
for some constants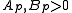
depending only on 
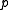(see Expected value
for notation). The sharp values of the constants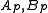
were found by Haagerup (Ref. 2; see Ref. 3 for a simpler proof).
. One example of its use in analysis
is the following: if we let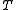
be a linear operator between two Lp spaces
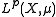and 
, 
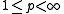, with bounded norm
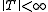, then one can use Khintchine's inequality to show that
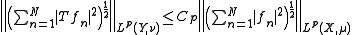
for some constant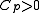
depending only on 
and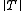 
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Khintchine inequality, named after Aleksandr Khinchin and spelled in multiple ways in the Roman alphabet, is a theorem from probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
, and is also frequently used in analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
. Heuristically, it says that if we pick
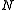complex numbers 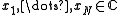, and add them together each multiplied by a random sign 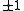, then the expected valueExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of its modulus
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
, or the modulus it will be closest to on average, will be not too far off from
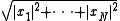.Statement of theorem
Let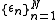 be i.i.d. random variableswith
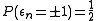for every 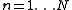,i.e., a sequence with Rademacher distribution.
Let
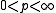and let 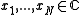.Then
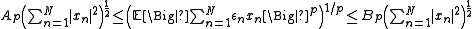
for some constants
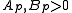depending only on 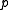(see Expected valueExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
for notation). The sharp values of the constants
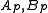were found by Haagerup (Ref. 2; see Ref. 3 for a simpler proof).Uses in analysis
The uses of this inequality are not limited to applications in probability theoryProbability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
. One example of its use in analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
is the following: if we let
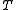be a linear operator between two Lp spacesLp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
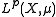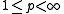and , , with bounded normOperator norm
In mathematics, the operator norm is a means to measure the "size" of certain linear operators. Formally, it is a norm defined on the space of bounded linear operators between two given normed vector spaces.- Introduction and definition :...
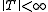, then one can use Khintchine's inequality to show that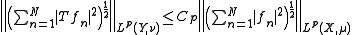for some constant
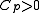depending only on and 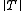.